7

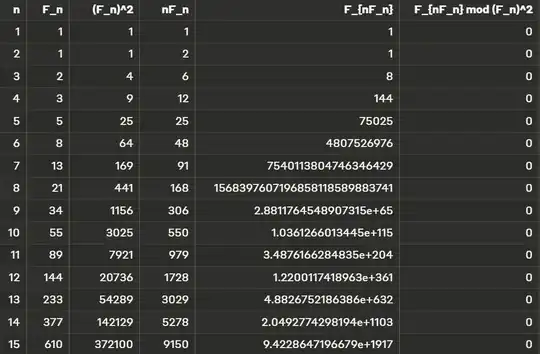
Is there a proof or a counterexample for the theorem that states: For all positive integers $n$, $(F_n)^2$ divides $F_{nF_n}$, where $F_n$ denotes the $n$th Fibonacci number? I believe this theorem is true. Here's my attempt at a proof by induction: Let $P(n)$ be the proposition: $(F_n)^2 \mid F_{nF_n}$. Base case: $P(3)$ is true, as $(F_3)^2 = 2^2 = 4$ divides $F_{3F_3} = F_6 = 8$. Inductive step: Assume $P(n)$ is true, i.e., $(F_n)^2 \mid F_{nF_n}$. We need to prove $P(n+1)$, i.e., $(F_{n+1})^2 \mid F_{(n+1)F_{n+1}}$. Using the Fibonacci recurrence relation $F_{r+s} = F_{r-1}F_s + F_rF_{s+1}$, we have

$$F_{(n+1)F_{n+1}} = F_{nF_{n+1} + F_{n+1}} = F_{nF_{n+1}-1} F_{F_{n+1}} + F_{nF_{n+1}}F_{F_{n+1}-1}.$$

At this point, I'm not sure how to proceed with the proof. I can't see a clear way to use the induction hypothesis to show that $(F_{n+1})^2$ divides this expression. Could someone provide guidance on how to complete this proof, or if there's a flaw in my approach? Alternatively, if this theorem is false, a counterexample would be greatly appreciated. enter image description here

C Pat
  • 389
  • 1
    Fascinating question. By the way, you can write $(F_n)^2$ as $F_n^2$ with F_{n}^{2}. In fact the braces are optional, as each pair contains only one character, so F_n^2 suffices. – J.G. Sep 19 '24 at 07:48
  • Follows easily by LTE/Hensel, e.g. see the linked dupe (put $,k= F_n,\ d = 2).\ \ $ – Bill Dubuque Sep 19 '24 at 16:02

1 Answers1

9

I think it is true. In fact, we can use the following Proposition:

If $F_1=1,F_2=1,F_{n}=F_{n-1}+F_{n-2}$, $\forall n\ge 3$, then for any $d,n\in \mathbb{N}$, $\gcd(n,F_d)F_d\mid F_{dn}$.

Choose $F_n$ and $n$, we have $F^2_n=\gcd(F_n,F_n)F_n\mid F_{nF_n}.$

Proof of this Proposition: Let $A=\left( \begin{matrix} 0& 1\\ 1& 1\\ \end{matrix} \right) ,B=I_2-A,\mathcal{F} =\left\{ aA+bI_2\mid a,b\in \mathbb{Z} \right\} $, then $A-B\in \mathcal{F}$.

By the induction,we can prove $A^n=F_nA+F_{n-1}I_2$, $B^n=F_nB+F_{n-1}I_2$. Thus $A^n-B^n=F_n(A-B)$.

We also need the following lemma:

Let $R$ be a commutative ring with an identity, and let $u$ and $n$ be two nonnegative integers. Let $x, y \in R$ be two elements such that $x − y \in uR$, then $x^n-y^n\in guR$, where $g=\gcd(n,u)$.

By this lemma, let $R=\mathcal{F}, x=A^d,y=B^d$, since $A^d-B^d=F_d(A-B)$, then $F_{dn}(A-B)=A^{dn}-B^{dn}\in gF_d\mathcal{F}$.

There exists $\alpha\in\mathcal{F}$ such that $F_{dn}(A-B)=gF_d\alpha.$

Assume that $(\alpha)_{22}=m\in \mathbb{Z}$,since $(A-B)_{22}=1$, we have $g\cdot F_d\cdot m=F_{dn}.$ In other words, $\gcd(n,F_d)F_d\mid F_{dn}$.

J.G.
  • 118,053
fusheng
  • 1,238
  • your proposition is a nice generalisation of the well known fact that $F_n \mid F_{dn}$ for $d\ge1$ – tkw Sep 19 '24 at 10:45