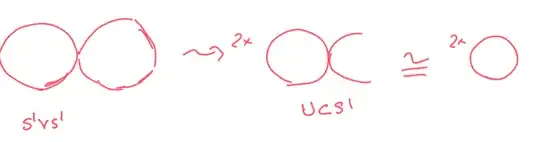In applying the Van Kampen theorem to the figure 8 / Wedge sum of circles, the following decomposition of the figure in open sets is used:
Intuitively I think I understand how they are both homotopy equivalent to each other. Let $X$ denote the circle with the cup on it's head, and $Y$ denote the circle. We denote $g$ as the embedding of the circle in $X$, and $f$ as the map which sends the points on the circle part of $X$ to the circle and the points on the cup part to the point where the cup meets the circle part of $X$.
My problem is how to formalize this?
My attempts at formalizing
I can pretty easily formalize $U$. Consider the point $p$ where the two circles touch. We can consider an open set containing it and then union with entire of either of the circles.
I think if one fits in $X$ and $Y$ as subspaces into $\mathbb{R^2}$ I think it is possible to give an expression for the homotopy in cartesian coordinates, but I wonder if there is a more "moral way". I think we should be able to do this without seeing the objects in ambient space of $\mathbb{R^2}$
Perhaps we could show that $X$ is homeomorphic to the space formed by attaching an open interval to a circle. Then calculate the fundamental group of the wedge sum but theorems involving general fundamental group of wedge sum is quite complicated.
Remark: A similar issue comes up when showing that $S^2 \wedge S^2$
Note: I will appreciate even a textbook reference where such constructions are done in high detail. The references I found (eg: Hatcher) don't explain enough, and neither does references that I can find in Internet.
I also searched entirety of MSE for a post explainign this point but I could not find any...