Let $m,n\in \mathbb N$ and $m\geq 1$. Let $R_{m,n}$ be the equivalence relation $$ xR_{m,n}y \Leftrightarrow x=y \quad \text{or} \quad (x\geq n \text{ and } y\geq n \text{ and } m\mid x-y) $$ in the set $\mathbb N$. I have shown that addition in the monoid $(\mathbb N, +)$ is compatible with the relation, so we can define the natural operation in the quotient monoid $\mathbb N/R_{m,n}$. We are asked to "describe the quotient monoid", but I'm having a hard time visualizing it.
Asked
Active
Viewed 67 times
2
-
Look at special cases (e.g. $n=0$ or $n=m$). Ask yourself questions (e.g. is the quotient finite?).Does the condition $m|x-y$ remind you of some other topic in algebra? – Stefan Sep 15 '24 at 14:02
-
The relations mean numbers are equal if they’re equal in N, or bigger than n and equivalent modulo m. So you’ll get {0,1, …,n} unaffected, and numbers bigger than n have the usual ‘modulo m’ relation. Putting this together, we get the set {0, … , n-1, [n], [n+1], …, [n+ m-1]}. Can you see how addition works? – Maximilien Mackie Sep 15 '24 at 14:05
-
Thanks, I realized the $m\mid x-y$ condition essentially grouped up integers like in $\mathbb Z/m\mathbb Z$, but for some reason it wasn't clear how this linked up with the condition $x=y$. – categoricallystupid Sep 15 '24 at 14:08
-
That's basically already an answer. – Martin Brandenburg Sep 15 '24 at 20:45
1 Answers
1
Here is the picture of the quotient, known in semigroup theory as the frying pan diagram.
$\hskip 60pt$
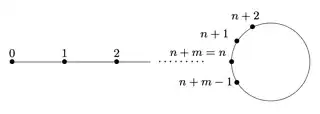
J.-E. Pin
- 42,871
-
Yes, thank you, this is what I pictured in my mind. Is it the case that every quotient monoid of $\mathbb N$ is necessarily of this form for some $n, m\in \mathbb N$ if we exclude quotienting by the trivial relations? – categoricallystupid Sep 21 '24 at 18:50
-
@cat a.k.a. $,\rho$ (vs. $\rm o),$ i.e. rho (vs. oh) shaped orbits, cf here and here and Pollards rho factorization algorithm, and reinventing the wheel (cycle). $\ \ $ – Bill Dubuque Sep 21 '24 at 18:50