Pascal gets drunk and builds his triangle. Half the time he writes $0$ instead of adding the two numbers above. What is the average of the numbers?

Question

One day Pascal has a little too much to drink, then sits down to build his famous triangle. He writes $1$'s going down the sides, no problem. Then he starts the arduous task of filling in the triangle. Each number is supposed to be the sum of the two numbers above it (and closest to it). But he's drunk, so half the time (probability $1/2$) he just writes $0$, and half the time he correctly adds the two numbers above it.

What is the expectation of the average (arithmetic mean) of all the numbers, for an infinitely large such triangle?

Simulations

I used Excel to build $5\times 10^6$ such triangles, with $20$ rows each.

{ Average of numbers in row $5$ } = $0.9998$
{ Average of numbers in row $10$ } = $0.9963$
{ Average of numbers in row $15$ } = $0.9940$
{ Average of numbers in row $20$ } = $0.9913$

I'm not sure what these data suggest.

Probability $1/2$ seems to be the critical value

I also did some simulations where the probability of Pascal writing $0$ is something other than $\frac12$. It seems that, if the probability is greater than $\frac12$ then the average of the numbers approaches $0$, and if the probability is less than $\frac12$ then the average of the numbers approaches infinity. Probability $\frac12$ seems to be the critical value.

Answer 1

Let $p$ be the probability that Pascal writes a zero instead of the sum in one of the interior entries of the triangle.

Let the top row (with only one single entry) be row $0$. If Pascal writes no zeros, the sum of entries on row $n$ is $2^n$.

Suppose $0 < p < 1$ and suppose Pascal writes a triangle. Let $X_n$ be the sum of row $n$ in the triangle and $X_{n+1}$ be the sum of row $n+1$.

If there were no zeros in row $n+1$ then we would have $X_{n+1} = 2X_n$. But the no-zeros version of row $n+1$ contains entries with total value $2X_n - 2$ (all entries excluding the $1$ at the start of the row and the $1$ at the end of the row), each of which can be deleted with probability $p$, so the expected value of row $n+1$ given that the sum of row $n$ is $x_n$ is

$$ \mathbb E(X_{n+1} \mid X_n = x_n) = 2x_n - (2x_n - 2)p = 2(1 - p)x_n + 2p. $$

Therefore $$ \mathbb E(X_{n+1}) = 2(1 - p)\mathbb E(X_n) + 2p, $$ which gives us a recurrence relation with the base case $\mathbb E(X_0) = 1.$

---

For $p=\frac12$ the recurrence is $$ \mathbb E(X_{n+1}) = \mathbb E(X_n) + 1. $$ The solution of the recurrence is therefore $\mathbb E(X_n) = n + 1$. Then $$ \mathbb E\left(\sum_{k=0}^n X_k\right) = \frac{(n + 1)(n + 2)}{2}, $$ which is also the total number of entries in rows $0$ through $n$ (inclusive), so the expected arithmetic mean of the numbers in a triangle whose last row is row $n$ is $1$.

As $n \to \infty$, then, $1 \to 1$.

The probability distribution of the mean is highly skewed, however, which can make it difficult to estimate the mean accurately using random sampling. Here are the results of one million repetitions of a python simulation of the sum of entries in a triangle up to row $5$. The theoretical mean sum is $21$, but sums slightly less than $21$ are more likely than sums slightly greater. I think this may help explain why you tended to find mean values less than $1$.

---

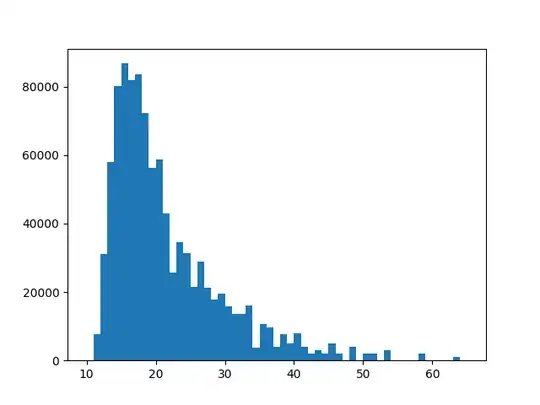
For $p \neq \frac12$ the solution of the recurrence is

$$ \mathbb E(X_n) = \frac{(2 - 2p)^n - 2p}{1 - 2p}. $$

Then

\begin{align} \mathbb E\left(\sum_{k=0}^n X_k\right) &= \sum_{k=0}^n \frac{(2 - 2p)^n - 2p}{1 - 2p} \\ &= -\frac{2(n+1)p}{1 - 2p} + \frac1{1 - 2p} \sum_{k=0}^n (2 - 2p)^n \\ &= -\frac{2(n+1)p}{1 - 2p} + \frac1{1 - 2p}\cdot\frac{(2-2p)^{n+1} - 1}{(2-2p) - 1} \\ &= \frac{(2-2p)^{n+1} - 1}{(1-2p)^2} - \frac{2(n+1)p}{1 - 2p}. \end{align}

The mean value of entries in rows $0$ through $n$ is therefore

\begin{multline} \frac{2}{(n+1)(n+2)} \left(\frac{(2-2p)^{n+1} - 1}{(1-2p)^2} - \frac{2(n+1)p}{1 - 2p} \right) \\ = \frac{2(2-2p)^{n+1} - 2}{(n+1)(n+2)(1-2p)^2} - \frac{4p}{(n+2)(1 - 2p)}. \end{multline}

If $p < \frac12$ then $2 - 2p > 1$ and the exponential function in the numerator of the first term, $(2-2p)^{n+1}$, dominates the polynomial in its denominator; so as $n \to +\infty$, \begin{align} \frac{2(2-2p)^{n+1} - 2}{(n+1)(n+2)(1-2p)^2} &\to +\infty, \\ \frac{4p}{(n+2)(1 - 2p)} &\to 0, \end{align} so the mean value goes to $+\infty$ as $n$ goes to $+\infty$.

If $p > \frac12$ then $0 \leq 2 - 2p < 1$ and $(2-2p)^{n+1} \to 0$ as $n \to +\infty$. Then as $n\to\infty$, $$\frac{2(2-2p)^{n+1} - 2}{(n+1)(n+2)(1-2p)^2} \to 0, $$ so the mean value goes to $0$ as $n$ goes to $+\infty$.

Answer 2

(This is based on @Karl's comment to the OP.)

The expectation of each number in row $2$ (which has three numbers, including the side $1$'s), is $1$.

So the expectation of each number in row $3$, is also $1$. This is because the expectation of each number is the average of the expectations of the two numbers above it.

And so on.

So the expectation of the average of all the numbers is $1$.

Is it that simple?

---

Edit: To show that this method does not always work (see comments), consider the following problem. Each number inside the triangle is the sum of the two numbers above it with probability $1/2$, and is the absolute value of the difference between the two numbers above it with probability $1/2$. Using the method above, we would conclude that the expectation of the average of all the numbers is $1$, but experimental results strongly suggest that the expectation of the average approaches infinity as the number of rows approaches infinity.

Answer 3

EDIT: I did have $p$ as the probability of keeping nonzero, which clashes with another answer. I now have

$p$ is the probability of writing 0.

But my reason for editing is to note that, if $2p\gt1$, then the first few averages in each row, (and the last few, in reverse), approach $$1,q,q^2,q^3,\ldots\\q=\frac{1-p}p$$ Assuming there is a limit, $q$ must satisfy $q=(1-p)(1+q)$. Then each limit is $q$ times the previous one.

End of edit

There is a contribution from each $1$ on the sides, when they are high enough.

$$\sum_{k=r-1}^{n-2}{k\choose r-1}(1-p)^{k+1}+\sum_{k=n-r-1}^{n-2}{k\choose n-r-1}(1-p)^{k+1}$$

The sum down to the $n$th row, excluding the $1$s, is
$$\sum_{k=1}^{n-1} k(2-2p)^{n-k}\\=\frac{(2-2p)^{n+1}-4n(1-p)^2+2(n-1)(1-p)}{(2p-1)^2}$$

So the sum of each row averages out to $2(1-p)/(2p-1)$ provided $2p\gt1$, or $2p/(2p-1)$ including the $1$s.