2

I was reading a paper that claims if $K, H \in \mathbb{R}^{n \times n}$, with both matrix being positive semidefinite, then $K = HW$ for some matrix $W$ iff $\operatorname{im} K \subseteq \operatorname{im} H$. I felt this can be proved by eigenvalue decomposition. However, I wonder if a more general statement can be made.

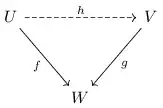
On a vector space $X$ (possibly infinite dimension) if we have two linear operators $K,H:X\to X$. Then does $\operatorname{im} K \subseteq \operatorname{im} H$ if and only if $K = H \circ W$ for some linear operator $W:X \to X$?

I cannot think of a way to prove this. In the finite dimensional case, I guess one can maybe do something such as SVD, but I felt there are simple way to prove it, or counterexamples.

patchouli
  • 1,996
  • I cannot think of a solution without using a basis of $X$ (so I think we need AC). However, if you are ok with using AC its doable: Think about how $W$ has to look, i.e. what it should do with the basis. – schiepy Sep 10 '24 at 17:31
  • @schiepy Even with a basis, you still need AC after that. (After all, $W$ can be non-injective, and you’d need to choose an element of the pre-image.) In fact, the case where $X$ admits a basis is enough to imply AC itself. – David Gao Sep 10 '24 at 18:02

1 Answers1

3

More generally, let $f : U \to W$, $g : V \to W$ be two linear maps with $\mathrm{im}(f) \subseteq \mathrm{im}(g)$. Let $B$ be a basis* of $U$. For every $b \in B$ there is therefore some $v \in V$ with $f(b)=g(v)$. So we find* a map $h' : B \to V$ with $f(b)=g(h(b))$ for all $b \in B$. Since $B$ is a basis of $U$, there is a unique linear map $h : U \to V$ with $h|_B = h'$. Then we have $f = g \circ h$ since these are linear maps that coincide on a basis.

commutative diagram

More generally, in any abelian category assume that $f : U \to W$, $g : V \to W$ are morphisms such that $\mathrm{im}(f) \subseteq \mathrm{im}(g)$, and assume that $U$ is projective. Then we may lift the corestricted morphism $f' : U \to \mathrm{im}(g)$ along the epimorphism $g' : V \to \mathrm{im}(g)$ to a morphism $h : U \to V$ with $f' = g' \circ h$. Composing with $\mathrm{im}(g) \hookrightarrow W$ yields $f = g \circ h$.

*This requires the axiom of choice if we want to prove this statement for all vector spaces $U$.

Martin Brandenburg
  • 181,922
  • the existence of a basis in the infinite dimensional case may, but need not, require AC. – Arturo Magidin Sep 10 '24 at 23:11
  • 1
    @ArturoMagidin https://dept.math.lsa.umich.edu/~ablass/bases-AC.pdf – Martin Brandenburg Sep 10 '24 at 23:11
  • I know that the existence of bases for arbitrary vector spaces is equivalent to AC. But here you have a vector space. Whether that vector space has a basis may require AC, but depending on what vector space $U$ is, it may not. The existence of a basis for $\mathbb{R}[x]$ does not require the invocation of AC. So the footnote, stating that you will, definitely, absolutely, need to use AC when $U$ is infinite dimensional is less than accurate. You may need to invoke it, but not necessarily. – Arturo Magidin Sep 10 '24 at 23:17
  • 2
    Yes, of course. But the question was about an arbitrary vector space. So I don't see the point of your comment. What do you want to add here to the answer? Feel free to edit it right away. – Martin Brandenburg Sep 10 '24 at 23:19
  • Are you happy now with the edit? – Martin Brandenburg Sep 10 '24 at 23:21
  • The point is that your footnote asserts that the Axiom of Choice will be required whenever $U$ is infinite dimensional in order to obtain a basis for $U$. That is not accurate. It would be accurate to say that "This may require the Axiom of Choice when $U$ is infinite dimensional." – Arturo Magidin Sep 10 '24 at 23:27
  • 2
    First of all, I am not completely sure if you are interested in improving my post or are just upset about me because of other comments and posts. If the latter is the case, please stop commenting now and come back tomorrow. Secondly, I believe that, what I wrote, is perfectly fine, easy to understand, and a valid way of stating that the AC is required for proving that all infinite-dimensional vector spaces have a basis (I write "general vector space" in the edit). Again: if you don't think so, please make an edit. But please avoid the wording "may". This is not mathematically accurate. – Martin Brandenburg Sep 10 '24 at 23:41
  • 1
    Just to put things into perspective, this is similar to the perfectly fine statement "the proof of n+m=m+n for natural numbers n,m requires induction" which you then criticize since the proof of 1+2=2+1 does not require induction. Of course we quantify over the free variables. – Martin Brandenburg Sep 10 '24 at 23:44