When proving the Cech-De Rham isomorphism on manifold $M$ with values in the constant presheaf $\mathbb R$ (Bott-Tu proposition 10.6):
$$ H^*(M,\mathbb R):=\lim_{\text{good covers }\mathcal U} H^*(\mathcal U,\mathbb R)\simeq H^{*}_{DR} (M) $$
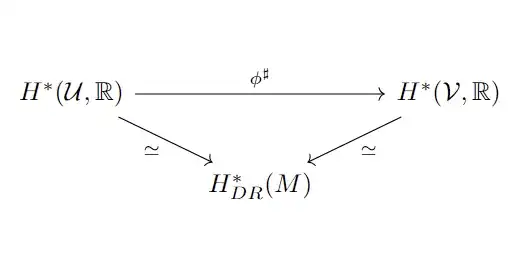
we need the following diagram to be commutative:
where $\mathcal U<\mathcal V$ are good covers and $\phi^{\sharp}$ is given by
$$ (\phi^{\sharp}\omega)(V_{\alpha_0...\alpha_n})=\omega(U_{\phi(\alpha_0)...\phi(\alpha_n)}) $$
if $V_{\alpha}\subseteq U_{\phi(\alpha)}$.
My question is how to prove the diagram commutes? A related question suggests that I should follow the collating formula to see that it restricts correctly, but I'm quite confused on why it restricts correctly and would like to see a more explicit explanation to it. Any help is very appreciated!