8

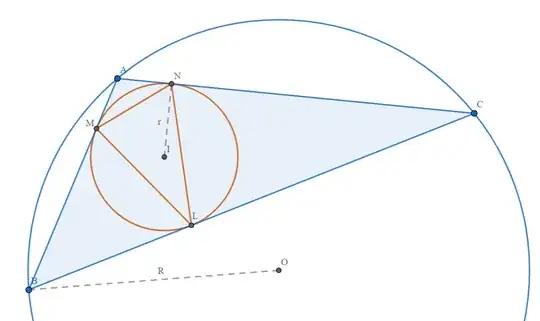
I have recently been reading "Advanced Euclidean Geometry" [ Posamentier , Wiley , 2002 ] and I just finished the chapter about equicircles. However, I got stuck on a problem for a while. Here it is:

"Prove that the ratio of the area of a triangle to the area of the triangle determined by the points of tangency of the incircle equals the ratio of twice the length of the circumradius to the length of the inradius of the given triangle."

A graph of the problem

I have tried using mainly the following formulas:

4R - r = r1 + r2 + r3 (where R is the circumradius, r is the inradius and r1,r2,r3 are the exradii of the triangle)

rs = Area of given triangle ABC (where s is the semiperimeter)

R = abc/4rs (where a,b,c are the sides of the triangle)

And many others depending on what seemed necessary. Nevertheless, my main problem has been that I have been able to neither recall nor find any relation between the area of the triangle determined by the points of tangency of the incircle and any other part or property of the given triangle.

I will be very grateful for any advice that involves neither analytic geometry, vectors, nor trigonometry!

Prem
  • 14,696
Martin Samanez
  • 125

2 Answers2

5

Briefly, demonstrating if $I$ and $O$ are on the same side or otherwise:

  1. Extend $BO$ to a circumdiameter $BB'$, and note the right-angled triangles $\triangle BB'A$ and $\triangle BB'C$. Let $k_C$ be the ratio of lengths $AB=c$ to circumdiameter $2R$, and $k_A$ be the ratio of $BC=a$ to $2R$:

$$\begin{align*} k_C &= \frac{c}{2R}\\ k_A &= \frac{a}{2R}\\ \end{align*}$$

  1. (As $I$ and $O$ are on the same side of $AB$) Trace angles $\angle BB'A = \angle BCA = 180^\circ - \angle LIN$.
    (As $I$ and $O$ are on opposite sides of $BC$) Trace angles $\angle BB'C = 180^\circ - \angle BAC = \angle NIM$.

  2. Find the ratio of areas of $\triangle AIB$ and $\triangle LIN$:

$$\begin{align*} \text{Area of }\triangle AIB &= \frac12 IM\cdot AB=\frac12 r\cdot 2Rk_C\\ \text{Area of }\triangle LIN &= \frac12 IL \cdot (\text{altitude from $N$ to $IL$})\\ &= \frac12 r\cdot rk_C\\ \frac{\text{Area of }\triangle AIB}{\text{Area of }\triangle LIN} &= \frac{2R}r \end{align*}$$

  1. Find the ratio of areas of $\triangle BIC$ and $\triangle NIM$:

$$\begin{align*} \text{Area of }\triangle BIC &= \frac12 IL\cdot BC=\frac12 r\cdot 2Rk_A\\ \text{Area of }\triangle NIM &= \frac12 IN \cdot (\text{altitude from $M$ to $IN$})\\ &= \frac12 r\cdot rk_A\\ \frac{\text{Area of }\triangle BIC}{\text{Area of }\triangle NIM} &= \frac{2R}r \end{align*}$$

  1. Similarly, the same ratio applies for the triangles in question:

$$ \frac{\text{Area of }\triangle AIB}{\text{Area of }\triangle LIN} = \frac{\text{Area of }\triangle BIC}{\text{Area of }\triangle NIM} = \frac{\text{Area of }\triangle CIA}{\text{Area of }\triangle MIL} = \frac{2R}r\\ \frac{\text{Area of }\triangle ABC}{\text{Area of }\triangle LNM} = \frac{2R}r $$

peterwhy
  • 22,930
5

Let us try to find an expression for the area of the Gergonne triangle:

$$\begin{align} \text{Area of } \triangle LMN &= \text{Area of } \triangle LIN+ \text{Area of } \triangle NIM+ \text{Area of } \triangle MIL \\ &= \frac 12 (IL \cdot IN \cdot \sin(\angle LIN)+IN \cdot IM \cdot \sin(\angle NIL)+IM \cdot IL \cdot \sin(\angle MIL)) \\ &= \frac 12 r^2 (\sin(\angle C)+\sin(\angle A)+\sin(\angle B)) \end{align}$$

Now, we can finish the proof using the Law of Sines: $$\begin{align} \frac{\text{Area of } \triangle ABC}{\text{Area of } \triangle LMN} &= \frac{rs}{0.5r^2 (\sin(\angle C)+\sin(\angle A)+\sin(\angle B))} \\ &= \frac{a+b+c}{r(\sin(\angle C)+\sin(\angle A)+\sin(\angle B))} \\ &= \frac{2R(\sin(\angle C)+\sin(\angle A)+\sin(\angle B))}{r(\sin(\angle C)+\sin(\angle A)+\sin(\angle B))}\\ &= \boxed{\frac{2R}{r}} \tag*{$\blacksquare$} \end{align}$$

D S
  • 5,642