Solve the inequality $\frac{2x-1}{x+2} \geq \frac{3x-1}{x+3}$

Question

To solve the inequality $\dfrac{2x-1}{x+2} \geq \dfrac{3x-1}{x+3}$, I multiplied in form of $x$ and got that $\begin{align*}(2x-1)(x+3) \geq (3x-1)(x+2)&\implies 2x^2+6x-x-3 \geq 3x^2+6x -x-2\\&\implies x^2 \leq -1\end{align*}$

I know that if we take it with basic knowledge there is no solution, but my question is what is the answer in complex numbers.

You've assumed $(x+2)(x+3)>0$. Now check the case where $(x+2)(x+3)<0$. — J.G., Sep 01 '24 at 18:06
To solve rational inequality, one has to be careful on the sign of the denominator. Explicitly, in your case, when you multiply $(x+3)$ to the left, and $(x+2)$ to the right (equivalently $(x+2)(x+3)$ to both sides), you did not change your sign, but $x+3$ and $x+2$ can be positive or negative. Therefore, in the first $\implies$, you already preassume $(x+2)(x+3)>0$, which make you lose some solution.
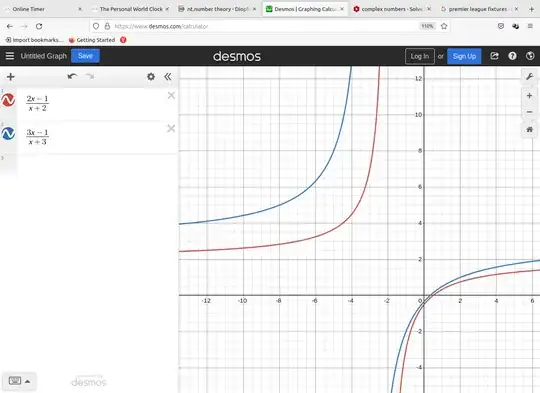
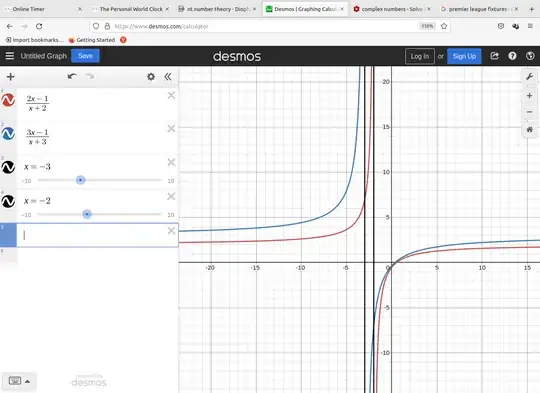
A possible way of doing this is to consider the cases $x<-3,-3<x<-2,x>-2$. — Angae MT, Sep 01 '24 at 18:13

score 2 · Accepted Answer · answered Sep 01 '24 at 18:44

2

The problem doesn't make sense in complex numbers, where there is no natural $\le$.

As for the real numbers, there is indeed no solution such that $(x+3)(x+2)>0$, but for $(x+3)(x+2)<0$ your inequation is equivalent to $x^2\ge-1$, which always holds. So, the set of solutions is $(-3,-2)$.

answered Sep 01 '24 at 18:44

Anne Bauval

49,005

@MSEU No: if $x\notin\Bbb R$ then $\frac{2x-1}{x+2}=2-\frac5{x+2}\notin\Bbb R$ and $\frac{3x-1}{x+3}=3-\frac{10}{x+3}\notin\Bbb R$. – Anne Bauval Sep 01 '24 at 20:30

score 1 · Answer 2 · 2024-09-01T20:04:50.667

1

$$\frac{2x-1}{x+2}-\frac{3x-1}{x+3}=-\frac{x^2+1}{(x+2)(x+3)}.$$

So this expression is positive when the denominator is negative (between $-3$ and $-2$).

edited Sep 01 '24 at 20:04

answered Sep 01 '24 at 19:57

score 0 · Answer 3 · answered Sep 01 '24 at 18:21

but my question is what is the answer in complex numbers.

None, it would be a "bad" problem. Inequalities like $\leq$ don't have a standard definition on complex numbers. It's possible to define some orderings, but none of them have all the usual properties we expect like $a>0, b>0 \implies ab>0$. See for example this Q&A.

score 0 · Answer 4 · answered Sep 01 '24 at 19:40

the graphs of the two indicated functions are hyperbolas; the red curve is $y = \frac{2x-1}{x+2} .$
For $x$ between $-3$ and $-2$ the red curve (upper arc) is higher than the blue curve (lower arc). For $x < -3$ the blue curve is higher, both upper arc. For $x > -2$ the blue curve is higher, both lower arc.

is lower for $x < -3$

Solve the inequality $\frac{2x-1}{x+2} \geq \frac{3x-1}{x+3}$

4 Answers4