Integral concerning the floor function

Question

I have a problem with the following integral: $$ \int_{1}^{\infty}\frac{\sin\left(\frac{\pi}{2}\{x\}\right)^{[x]}}{[x]}\cos\left(\frac{\pi}{2}\{x\}\right)\,dx $$ where $[x]$ is the floor function and $\{x\}:=x-[x]$. I tried to solve it using the following idea.

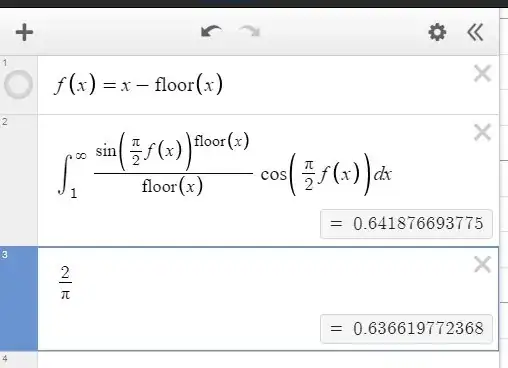
\begin{align} \int_{1}^{\infty}\frac{\sin\left(\frac{\pi}{2}\{x\}\right)^{[x]}}{[x]}\cos\left(\frac{\pi}{2}\{x\}\right)\,dx &= \int_{1}^{\infty}\frac{\sin\left(\frac{\pi}{2}(x-[x])\right)^{[x]}}{[x]}\cos\left(\frac{\pi}{2}(x-[x])\right)\,dx\\ &=\sum_{k=1}^{\infty}\int_{k}^{k+1}\frac{\sin\left(\frac{\pi}{2}(x-k)\right)^{k}}{k}\cos\left(\frac{\pi}{2}(x-k)\right)\,dx\\ &=\sum_{k=1}^{\infty}\frac{1}{k}\int_{0}^{1}\sin\left(\frac{\pi}{2}x\right)^{k}\cos\left(\frac{\pi}{2}x\right)\,dx\\ &=\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{1}{k}\int_{0}^{\pi/2}\sin(x)^k\,\cos(x)\,dx\\ &=\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{1}{k}\left(\frac{\sin(x)^{k+1}}{k+1}\right|_{0}^{\pi/2}\\ &=\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{1}{k\,(k+1)}=\frac{2}{\pi}. \end{align}

Now, I looked it up on Desmos and it tells me that this is wrong. In fact, as you can see in the image, the integral and my result are different.

Did I do something wrong? Thanks for any help.

Answer 1

Verification:

$$\begin{align} \int_{1}^{\infty}\frac{\sin\left(\frac{\pi}{2}\{x\}\right)^{[x]}}{[x]}\cos\left(\frac{\pi}{2}\{x\}\right)\,dx &=\sum_{k=1}^\infty\int_0^1\frac{\sin\left(\frac{\pi}{2}x\right)^k}k\cos\left(\tfrac{\pi}{2}x\right)\,dx \\&=\frac2\pi\sum_{k=1}^\infty\left.\frac{\sin\left(\frac{\pi}{2}x\right)^{k+1}}{k(k+1)}\right|_0^1\\&=\frac2\pi\sum_{k=1}^\infty\frac{1}{k(k+1)}. \end{align}$$

---

Given the tortuous shape of the function and its angular points, plus the slow decay, it is more than likely that numerical evaluation of this improper integral is challenged.

You might ask Desmos to evaluate on a few $[k,k+1]$ intervals. (WA replies exact values.)

Answer 2

Let $$f(x)=\frac{\sin\left(\frac{\pi}{2}\{x\}\right)^{[x]}}{[x]}\cos\left(\frac{\pi}{2}\{x\}\right)$$ and use Mathematica with the following syntax

R[p_]:=NIntegrate[f[x], {x, 1, Infinity}, WorkingPrecision -> p]

There is no problem or warning. Nice but the result depends very much on the value of the working precision $$\left( \begin{array}{cc} p & R(p) \\ 10 & 0.6317221476 \\ 20 & 0.6300419923 \\ 30 & 0.6319526217 \\ 40 & 0.6321773132 \\ 50 & 0.6327733152 \\ 60 & 0.6319059416 \\ 70 & 0.6320912143 \\ 80 & 0.6317180264 \\ 90 & 0.6318379131 \\ 100 & 0.6329749100 \\ 200 & 0.6326666679 \\ 300 & 0.6322638105 \\ 400 & 0.6321032001 \\ 500 & 0.6321174712 \\ 600 & 0.6322364980 \\ 700 & 0.6322364980 \\ \end{array} \right)$$

Even when the result stabilizes, we are still far away from $\frac 2 \pi$

Answer 3

At least quad manages to get $1/L$ convergence (as one would expect) after providing guiding in form of manual support points at $1,2,3,\dots$, and the limit does indeed appear to be $\frac{2}{\pi}$. Still, a direct numerical evaluation does not appear to be too favorable. Probably one should first transform the integral in some way.

Code to reproduce the figure:

import numpy as np
from scipy.integrate import quad
import matplotlib.pyplot as plt
Lv = np.unique(np.geomspace(1e1, 1e4, 20, dtype=int))
points = np.arange(1,Lv[-1]+1)
f = lambda x: np.sin(np.pi/2(x-np.floor(x)))np.floor(x)/np.floor(x)  np.cos(np.pi/2*(x-np.floor(x)))
y = np.array([quad(f, 1, L, limit=1<<16)[0] for L in Lv])
y2 = np.array([quad(f, 1, L, limit=1<<16, points=points[:L])[0] for L in Lv])
fig, ax = plt.subplots()
ax.plot(Lv, np.abs(y - 2/np.pi), label="naive quad", ls='', marker='o')
ax.plot(Lv, np.abs(y2 - 2/np.pi), label="quad with manual support", ls='', marker='o')
ax.set_xlabel(r"$L$")
ax.set_ylabel(r"$|I - \frac{2}{\pi}|$")
ax.set_xscale("log")
ax.set_yscale("log")
ax.legend()
```