Find the rotation angle of an Ellipse for a given point with horizontal tangent

Question

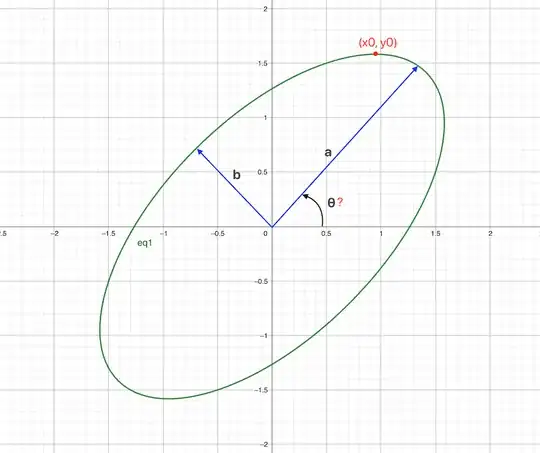
Suppose I have an ellipse centered at (0,0), defined by its major axis a, minor axis b, and a vertical extremum point (x0,y0). Is there a way to determine the rotation angle θ of the ellipse?

Answer 1

Method 1:

The extremum here is the maximum along the vertical direction.

The equation of this ellipse is

$ \mathbf{r}^T {R D R}^T \mathbf{r} = 1 $

where $\mathbf{r} = \begin{bmatrix} x \\ y \end{bmatrix} $ , $D = \begin{bmatrix} \dfrac{1}{a^2} && 0 \\ 0 && \dfrac{1}{b^2} \end{bmatrix} $

and $ R $ is a rotation matrix and is given by

$ R = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} $

Consider the unit vector in the vertical direction, it is named $\mathbf{j}$ and is given by

$ \mathbf{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} $

We now that at the extremum, the gradient of the ellipse (which is perpendicular to its curve) will be along $\mathbf{j}$. Therefore, if

$ \mathbf{r_0} = \begin{bmatrix} x_0 \\ y_0 \end{bmatrix} $

Then

$ {R D R}^T \mathbf{r_0} = c \mathbf{j} $

where $c \gt 0 $ is a constant. Solving for $\mathbf{r_0}$, we find that

$ \mathbf{r_0 } = c {R D^{-1} R}^T \mathbf{j} \tag{1} $

Since $\mathbf{r_0}$ is on the ellipse, it satisfies its equation, and therefore,

$ \mathbf{r_0}^T {R D R}^T \mathbf{r_0} = 1 $

which implies that

$ c^2 \mathbf{j}^T {R D^{-1} R}^T \mathbf{j} = 1 $

Therefore,

$ c= \dfrac{1}{\sqrt{\mathbf{j}^T {R D^{-1} R}^T \mathbf{j}} } $

It follows from $(1)$ that

$ \mathbf{r_0} = \dfrac{ {R D^{-1} R}^T \mathbf{j} }{ \sqrt{\mathbf{j}^T {R D^{-1} R}^T \mathbf{j} }} $

Therefore,

$ y_0 = \mathbf{j}^T \mathbf{r_0 } = \sqrt{\mathbf{j}^T {R D^{-1} R}^T \mathbf{j} } $

And,

$ x_0 = \mathbf{i}^T \mathbf{r_0} $

where $\mathbf{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} $

Now the matrix ${R D^{-1} R}^T$ is equal to

$ {R D^{-1} R}^T = \begin{bmatrix} a^2 \cos^2 \theta + b^2 \sin^2 \theta && \cos \theta \sin \theta (a^2 - b^2) \\ \cos \theta \sin \theta (a^2 - b^2) && a^2 \sin^2 \theta + b^2 \cos^2 \theta \end{bmatrix}$

Therefore,

$\mathbf{j}^T {R D^{-1} R}^T \mathbf{j} = a^2 \sin^2 \theta + b^2 \cos^2 \theta $

Hence,

$ a^2 \sin^2 \theta + b^2 \cos^2 \theta = y_0^2 $

Using the identities $\cos^2 \theta = \frac{1}{2} ( 1 + \cos(2 \theta)) $ and $\sin^2 \theta = \frac{1}{2} ( 1- \cos(2 \theta)) $, this becomes

$ \frac{1}{2}(a^2 + b^2) + \frac{1}{2} (b^2 - a^2) \cos(2 \theta) = y_0^2 $

So that

$ \theta = \frac{1}{2} \cos^{-1} \left( \dfrac{(a^2 + b^2) - 2 y_0^2 }{ a^2 - b^2 } \right) $

Assuming $ a \gt b $, this will have a real solution if and only if,

$ - (a^2 - b^2 ) \le a^2 + b^2 - 2 y_0^2 \le a^2 - b^2 $

i.e.

$ - 2 a^2 \le - 2 y_0^2 \le - 2 b^2 $

And finally,

$ b \le |y_0 | \le a $

Note that two angles $\theta$ are possible, which differ by a sign. To determine which one is the correct one, consider

$ x_0 = \mathbf{i}^T \mathbf{r_0} = \dfrac{ \mathbf{i}^T {R D^{-1} R}^T \mathbf{j} }{ \sqrt{ \mathbf{j}^T { R D^{-1} R}^T \mathbf{j} } } $

The numerator of the right hand side is just

$ \cos \theta \sin \theta (a^2 - b^2) $

Since $a^2 - b^2 \gt 0$, then we'll choose the correct $\theta$ based on the sign of $\cos \theta \sin \theta $ to be the same as the sign of $x_0$.

Method 2 (Much easier):

Remember that the parametric equation of the ellipse in standard position is

$ \mathbf{r}(t) = \begin{bmatrix} a \cos t \\ b \sin t \end{bmatrix} $

Therefore, the parametric equation of a rotated ellipse is

$ \mathbf{p}(t) = R \mathbf{r} = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} \begin{bmatrix} a \cos t \\ b \sin t \end{bmatrix} = \begin{bmatrix} a \cos \theta \cos t - b \sin \theta \sin t \\ a \sin \theta \cos t + b \cos \theta \sin t \end{bmatrix} $

The extremum in the vertical direction is found by maximizing the $y$ coordinate of the above vector, i.e. the maximum of

$$ a \sin \theta \cos t + b \cos \theta \sin t $$

And this maximum (over $t$) is given by

$ y_{\text{Max}} = \sqrt{ a^2 \sin^2 \theta + b^2 \cos^2 \theta } $

And this maximum is known from the given extremeum $(x_0, y_0) $. Therefore, we only need to solve the trigonometric equation

$ a^2 \sin^2 \theta + b^2 \cos^2 \theta = y_0^2 $

The rest is the same as in Method 1.