Solving $y'=\cos x \int \cos x^2 dx$

Question

This seems a very hard ODE that I couldn't solve.

It is from Zorich Mathematical Analysis so I guess there must be a somewhat-enlightening solution.

Though my half-attempt is here:

$$y'(x)=\cos x\int \cos x^2 dx$$ $$dy=\cos x(\int \cos x^2 dx) dx$$ $$y=\int \cos x(\int \cos x^2 dx)dx+C$$

Editted after 4 hours:

By using trigonometric series for $\cos x^2$ and $\cos x$

We get $$y(x)=\int \cos x\int \cos x^2 dx= \int \cos x\sum_{k=0}^\infty\frac{(-1)^kx^{4k+1}}{(2k)!(4k+1)} dx$$ $$y(x)=\sum_{k=0}^\infty \frac{(-1)^k \int x^{4k+1}\cos x dx}{(2k)!(4k+1)}$$

By adopting a power series approach again,

$$y(x)=\sum_{i,j=0}^\infty \frac{(-1)^j x^{2j+4k+2}}{(2k)!(2j)!(4k+1)(2j+4k+2)}$$

Now, my question is, is there a closed form for this? Or even, a better approach?

Answer 1

There should be no closed form but you could write $y$ as a different series, in terms of Fresnal integral or error functions, or use some close approximations. The representation via Fresnal integral or the error function brings $y$ into a more familiar form, the series expansion further makes work "easier" and approximations possible and with approximations the possible long calculation times could be avoided.

---

Solution via Fresnel integrals

Using one definition of the Fresnel integrals $\operatorname{C}\left( x \right) := \int_{0}^{x} \cos\left( t^{2} \right)\, \operatorname{d}t$ let's us simplify the equation: \begin{align*} y\left( x \right) &= \int \cos\left( x \right) \cdot \int \cos\left( x^{2} \right)\, \operatorname{d}x\, \operatorname{d}x = \int \cos\left( x \right) \cdot \left( \operatorname{C}\left( x \right) + \text{c}_{1} \right)\, \operatorname{d}x\\ &= \int \cos\left( x \right) \cdot \operatorname{C}\left( x \right)\, \operatorname{d}x + \int \cos\left( x \right) \cdot \text{c}_{1}\, \operatorname{d}x = \int \cos\left( x \right) \cdot \operatorname{C}\left( x \right)\, \operatorname{d}x + \text{c}_{1} \cdot \int \cos\left( x \right)\, \operatorname{d}x\\ &= \int \cos\left( x \right) \cdot \operatorname{C}\left( x \right)\, \operatorname{d}x + \text{c}_{1} \cdot \sin\left( x \right) + \text{c}_{2}\\ \end{align*}

We can rewrite $\int \cos\left( x \right) \cdot \operatorname{C}\left( x \right)\, \operatorname{d}x$ to $\int \cos\left( x \right) \cdot \operatorname{C}\left( x \right)\, \operatorname{d}x = \int_{0}^{x} \cos\left( t \right) \cdot \operatorname{C}\left( t \right)\, \operatorname{d}t + \text{c}_{3}$. Using integration by parts gives us: \begin{align*} I_{1} &:= \int_{0}^{x} \cos\left( t \right) \cdot \operatorname{C}\left( t \right)\, \operatorname{d}t = \left[ \int \cos\left( t \right) \, \operatorname{d}t \cdot \operatorname{C}\left( t \right) \right]_{0}^{x} - \int_{0}^{x} \int \cos\left( t \right) \, \operatorname{d}t \cdot \operatorname{C'}\left( t \right)\, \operatorname{d}t\\ &= \left[ \sin\left( t \right) \cdot \operatorname{C}\left( t \right) \right]_{0}^{x} - \int_{0}^{x} \sin\left( t \right) \cdot \cos\left( t^{2} \right)\, \operatorname{d}t = \sin\left( x \right) \cdot \operatorname{C}\left( x \right) - \sin\left( 0 \right) \cdot \operatorname{C}\left( 0 \right) - \int_{0}^{x} \sin\left( t \right) \cdot \cos\left( t^{2} \right)\, \operatorname{d}t\\ &= \sin\left( x \right) \cdot \operatorname{C}\left( x \right) - \int_{0}^{x} \sin\left( t \right) \cdot \cos\left( t^{2} \right)\, \operatorname{d}t\\ \end{align*} Integral-calculator.com can give you as step by step solution for $\int \sin\left( t \right) \cdot \cos\left( x^{2} \right)\, \operatorname{d}x$ (note: the site uses a different normalization then Wikipedia). Using $\sin\left( x \right) \cdot \cos\left( y \right) = \tfrac{\sin\left( x + y \right) - \sin\left( x - y \right)}{2}$ (Product-to-sum identity) let's us rewrite $\int \sin\left( t \right) \cdot \cos\left( x^{2} \right)\, \operatorname{d}x = \int \frac{\sin\left( x^{2} + x \right) - \sin\left( x^{2} - x \right)}{2}\, \operatorname{d}x = \frac{1}{2} \cdot \left( \int \sin\left( x^{2} + x \right)\, \operatorname{d}x - \int \sin\left( x^{2} - x \right)\, \operatorname{d}x \right)$. Let $I_{2} := \int \sin\left( x^{2} + x \right)\, \operatorname{d}x$ and $I_{3} := \int \sin\left( x^{2} - x \right)\, \operatorname{d}x$, then completing the square gives us $I_{2} = \int \cos\left( \left( x + \frac{1}{2} \right)^{2} - \frac{1}{4} \right)\, \operatorname{d}x$ and $I_{3} = \int \sin\left( \left( x - \frac{1}{2} \right)^{2} - \frac{1}{4} \right)\, \operatorname{d}x$. Substituting $t_{1} := x + \frac{1}{2} \Leftrightarrow \operatorname{d}t_{1} = \operatorname{d}x$ and $t_{2} := x - \frac{1}{2} \Leftrightarrow \operatorname{d}t_{2} = \operatorname{d}x$ gives us $I_{2} = \int \cos\left( t_{1}^{2} - \frac{1}{4} \right)\, \operatorname{d}t_{1}$ and $I_{3} = \int \sin\left( t_{2}^{2} - \frac{1}{4} \right)\, \operatorname{d}t_{2}$. Using $\sin\left( x - y \right) = \cos\left( x \right) \cdot \sin\left( y \right) - \cos\left( x \right) \cdot \sin\left( y \right)$ (angle addition identity) gives us: \begin{align*} I_{2} &= \int \sin\left( t_{1}^{2} - \frac{1}{4} \right)\, \operatorname{d}t_{1} = \int \left( \sin\left( t_{1}^{2} \right) \cdot \cos\left( \frac{1}{4} \right) - \cos\left( t_{1}^{2} \right) \cdot \sin\left( \frac{1}{4} \right) \right)\, \operatorname{d}t_{1}\\ &= \cos\left( \frac{1}{4} \right) \cdot \int \sin\left( t_{1}^{2} \right)\, \operatorname{d}t_{1} - \sin\left( \frac{1}{4} \right) \cdot \int \cos\left( t_{1}^{2} \right)\, \operatorname{d}t_{1}\\ &= \cos\left( \frac{1}{4} \right) \cdot \operatorname{S}\left( t_{1} \right) - \sin\left( \frac{1}{4} \right) \cdot \operatorname{C}\left( t_{1} \right)\\ I_{3} &= \int \sin\left( t_{2}^{2} - \frac{1}{4} \right)\, \operatorname{d}t_{2} = \int \left( \sin\left( t_{2}^{2} \right) \cdot \cos\left( \frac{1}{4} \right) - \cos\left( t_{2}^{2} \right) \cdot \sin\left( \frac{1}{4} \right) \right)\, \operatorname{d}t_{2}\\ &= \cos\left( \frac{1}{4} \right) \cdot \int \sin\left( t_{2}^{2} \right)\, \operatorname{d}t_{2} - \sin\left( \frac{1}{4} \right) \cdot \int \cos\left( t_{2}^{2} \right)\, \operatorname{d}t_{2}\\ &= \cos\left( \frac{1}{4} \right) \cdot \operatorname{S}\left( t_{2} \right) - \sin\left( \frac{1}{4} \right) \cdot \operatorname{C}\left( t_{2} \right)\\ \end{align*} where $\operatorname{S}\left( x \right) := \int_{0}^{x} \sin\left( t^{2} \right)\, \operatorname{d}t$ is another Fresnal integral. Re-substituting everything gives us: $$\fbox{$ y\left( x \right) = \cos\left( \frac{1}{4} \right) \cdot \frac{\operatorname{S}\left( x - \frac{1}{2} \right) - \operatorname{S}\left( x + \frac{1}{2} \right)}{2} + \sin\left( \frac{1}{4} \right) \cdot \frac{\operatorname{C}\left( x + \frac{1}{2} \right) - \operatorname{C}\left( x - \frac{1}{2} \right)}{2} + \left( \text{c}_{1} + \operatorname{C}\left( x \right) \right) \cdot \sin\left( x \right) + \text{c}_{2} $}$$

You can compare the plots here on Desmos. You can write the Fresnal integrals in terms of Error functions if you like that more.

Other series solution

We know $y\left( x \right) = \int \cos\left( x \right) \cdot \int \cos\left( x^{2} \right)\, \operatorname{d}x\, \operatorname{d}x$. The Equation is transformable into a linear ODE of second order, so we can assume two initial conditions $y\left( 0 \right) =: y_{0}$ and $y'\left( 0 \right) =: y_{1}$. The Taylor series of $y$ around $x = 0$ is definiend by $y\left( x \right) = \sum_{k = 0}^{\infty}\left[ \frac{y^{\left( k \right)}\left( 0 \right)}{k!} \cdot x^{k} \right]$. Taking the derivatives: \begin{align*} y\left( x \right) &= \int \cos\left( x \right) \cdot \int \cos\left( x^{2} \right)\, \operatorname{d}x\, \operatorname{d}x\\ y'\left( x \right) &= \cos\left( x \right) \cdot \int \cos\left( x^{2} \right)\, \operatorname{d}x\\ y''\left( x \right) &= \cos'\left( x \right) \cdot \int \cos\left( x^{2} \right)\, \operatorname{d}x + \cos\left( x \right) \cdot \cos\left( x^{2} \right)\\ &~~\vdots\\ y^{\left( k \right)}\left( x \right) &= \sum\limits_{g = 0}^{k}\left[ \binom{k}{g} \cdot \cos^{\left( k - g \right)}\left( x \right) \cdot \operatorname{D}_{x}^{g}\left[ \int \cos\left( x^{2} \right)\, \operatorname{d}x \right] \right]\\ \end{align*} where $\operatorname{D}_{x}^{g} := \frac{\operatorname{d}^{g}}{\operatorname{d}x^{g}}$. You can that formula by induction or by using the general Leibniz rule. It's trivial that $\operatorname{D}_{x}^{g}\left[ \int \cos\left( x^{2} \right)\, \operatorname{d}x \right] = \operatorname{D}_{x}^{g - 1}\left[ \cos\left( x^{2} \right) \right]$ and by using Faà di Bruno's formula we get ($f\left( x \right) := x^{2}$): \begin{align*} \operatorname{D}_{x}^{g - 1}\left[ \cos\left( x^{2} \right) \right] &= \sum\limits_{n = 0}^{g - 1}\left[ \cos^{\left( n \right)}\left( f\left( x \right) \right) \cdot \operatorname{B}_{g - 1,\, n}\left( f^{\left( 1 \right)}\left( x \right),\, f^{\left( 2 \right)}\left( x \right),\, \ldots,\, f^{\left( g - 1 - n + 1 \right)}\left( x \right) \right) \right]\\ \end{align*} We know $f^{\left( n \right)}\left( x \right) = \begin{cases} \frac{2}{\left( 2 - n \right)!} \cdot x^{2 - n},\, &\text{for } n \leq 2\\ 0,\, &\text{for } n > 2\\ \end{cases}$ (you can see the proof here) and $\cos^{\left( n \right)}\left( x \right) = \cos\left( x + \frac{n}{2} \cdot \pi \right)$ which is also discused here. So (for $k \geq 2$): \begin{align*} y^{\left( k \right)}\left( x \right) &= \sum\limits_{g = 0}^{k}\left[ \binom{k}{g} \cdot \cos\left( x + \frac{k - g}{2} \cdot \pi \right) \cdot \sum\limits_{n = 0}^{g - 1}\left[ \cos\left( x^{2} + \frac{k - g}{2} \cdot \pi \right) \cdot \operatorname{B}_{g - 1,\, n}\left( 2 \cdot x,\, 2,\, \ldots,\, 0 \right) \right] \right]\\ y^{\left( k \right)}\left( 0 \right) &= \sum\limits_{g = 0}^{k}\left[ \binom{k}{g} \cdot \cos\left( \frac{k - g}{2} \cdot \pi \right) \cdot \sum\limits_{n = 0}^{g - 1}\left[ \cos\left( \frac{n}{2} \cdot \pi \right) \cdot \operatorname{B}_{g - 1,\, n}\left( 0,\, 2,\, \ldots,\, 0 \right) \right] \right]\\ \end{align*}

Approximation

We can say $\int_{0}^{x} \cos\left( t^{2} \right)\, \operatorname{d}t \approx \sqrt{\frac{\pi}{8}} + \frac{\sin\left( x^{2} \right)}{\sqrt{2 \cdot \pi} \cdot x} \wedge x \geq 1$ (see formula $11$ here). It follows $y\left( x \right) = \int \cos\left( x \right) \cdot \int \cos\left( x^{2} \right)\, \operatorname{d}x\, \operatorname{d}x \approx \int \cos\left( x \right) \cdot \left( \text{c}_{1} + \frac{\sin\left( x^{2} \right)}{\sqrt{2 \cdot \pi} \cdot x} \right)\, \operatorname{d}x = \text{c}_{1} \cdot \sin\left( x \right) + \int \frac{\cos\left( x \right) \cdot \sin\left( x^{2} \right)}{\sqrt{2 \cdot \pi} \cdot x}\, \operatorname{d}x$. We could use this for numeric integration. We could also rewrite the solution in terms of Fresnal integrals (if we use formula $12$ too) to: \begin{align*} y\left( x \right) &\approx \cos\left( \frac{1}{4} \right) \cdot \frac{\frac{\cos\left( \left( x + \frac{1}{2} \right)^{2} \right)}{\sqrt{2 \cdot \pi} \cdot \left( x + \frac{1}{2} \right)} - \frac{\cos\left( \left( x - \frac{1}{2} \right)^{2} \right)}{\sqrt{2 \cdot \pi} \cdot \left( x - \frac{1}{2} \right)}}{2} + \sin\left( \frac{1}{4} \right) \cdot \frac{\frac{\sin\left( \left( x + \frac{1}{2} \right)^{2} \right)}{\sqrt{2 \cdot \pi} \cdot \left( x + \frac{1}{2} \right)} - \frac{\sin\left( \left( x - \frac{1}{2} \right)^{2} \right)}{\sqrt{2 \cdot \pi} \cdot \left( x - \frac{1}{2} \right)}}{2} + \left( \text{c}_{1} + \sqrt{\frac{\pi}{8}} + \frac{\sin\left( x^{2} \right)}{\sqrt{2 \cdot \pi} \cdot x} \right) \cdot \sin\left( x \right) + \text{c}_{2}\\ \end{align*}

This is a little plot for this approximation ($c_{1} := 0.1 \wedge c_{2} := 0$): The red line is the Solution via Fresnel integrals minus it's value at zero and the blue line is the approximation.

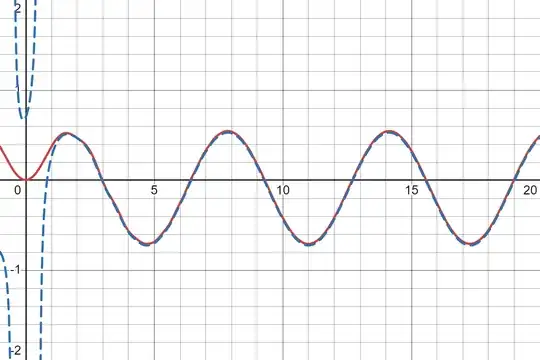
You can check it here on Desmos.

Answer 2

Mathematica:

$$\frac{1}{8} \sqrt[4]{-1} e^{-\frac{i}{4}} \sqrt{\pi } \left(-e^{\frac{i}{2}} \left(\text{erf}\left(\frac{1}{2} \sqrt[4]{-1} (1-2 x)\right)+\text{erf}\left(\frac{1}{2} \sqrt[4]{-1} (2 x+1)\right)\right)-i \left(\text{erf}\left(\frac{1}{2} (-1)^{3/4} (1-2 x)\right)+\text{erf}\left(\frac{1}{2} (-1)^{3/4} (2 x+1)\right)\right)\right)+\sqrt{\frac{\pi }{2}} C\left(\sqrt{\frac{2}{\pi }} x\right) \sin (x)+c_1$$

Answer 3

Zorich Mathematical Analysis can be downloaded

p. 369

Example 5. Suppose we need to compute the integral

$$ \int \sin(x^2) dx$$

for example within $10^{-2}$.

We know that the primitive $\int \sin(x^2) dx$ (the Fresnel integral) cannot be expressed in terms of elementary functions, so that it is impossible to use the Newton-Leibniz formula here in the traditional sense.

It would be nice, not to obscure a source by irregular mathematical notations and exchange cos for sin.