1

Let $n \in \mathbb Z_{\geq 3}$. While playing around in Mathematica I noticed the following limit $$B_n(x) \searrow 0 \qquad \text{as }\, x\to\infty,$$ where $B_n(x)$ is an alternating binomial-type expression of the form $$B_n(x) = - \sum_{k=0}^n (-1)^k \binom nk \zeta'\left(-1,\frac kn + x\right).$$ Here, $\zeta'\left(-1,a\right)$ is the Hurwitz Zeta function $\zeta\left(s,a\right)$ differentiated with respect to $s$ in $s=-1$. This function has a known 'alternative form' in terms of a few elemetary functions and a polygamma function: see for instance https://functions.wolfram.com/10.02.20.0023.01. (In our case, the '$\sum_{i=0}^{\lfloor{- \Re(a)}\rfloor}$' sum is empty as we are only interested in values, say, $x \geq 1$, to compute the limit.)

For example, if $n = 4$, then $$B_4(x) = -\zeta'\left(-1, x\right) + 4 \zeta'\left(-1,\frac 14 + x\right) - 6 \zeta'\left(-1,\frac 12 + x\right) + 4 \zeta'\left(-1,\frac 34 + x\right) -\zeta'\left(-1, 1+ x\right).$$ The reason for the leading minus sign is arbitrary, but then the graph of this function is positive when I plot it.

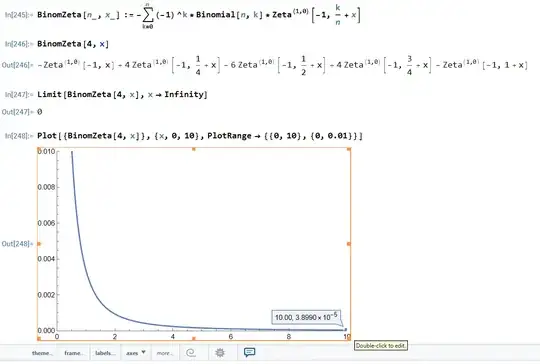
See the following screenshot I made from Mathematica:

enter image description here

My question is, does anybody recognize this limit? Or know of any results one could maybe use to prove it? (Any alternate forms to write $B_n(x)$?) Thanks!

(It looks a bit like The multiplication formula for the Hurwitz zeta function but with an $s$-derivative and binomial coefficients ...)

UPDATE

Using the alternate form of $\zeta'\left(-1,s\right)$ (from https://functions.wolfram.com/10.02.20.0023.01 ) it can be shown that we just need to prove that essentially the same thing is true but for the PolyGamma function: $$ \sum_{k=0}^n (-1)^k \binom nk \psi^{(-2)}\left(\frac kn + x\right) \longrightarrow 0 \quad \text{as} \quad x \to \infty. $$ (Grouping the other terms gives a function consisting of polynomials and logarithms and simplifying them gives $$ -((x-1) \log (x-1))+(4 x-3) \log \left(x-\frac{3}{4}\right)-6 x \log \left(x-\frac{1}{2}\right)+3 \log \left(x-\frac{1}{2}\right)+4 x \log \left(x-\frac{1}{4}\right)-\log \left(x-\frac{1}{4}\right)-x \log (x), $$ which I think you can compute the limit of by hand? (If you wanted to ...)) Maybe this helps?

Neckverse Herdman
  • 1,746

1 Answers1

1

I believe I have resolved this now

Using http://functions.wolfram.com/06.15.06.0044.01 for $n=2$, we have a nice asymptotic value: $$\psi ^{(2)}(x) = \log (A)-\frac{3 x^2}{4}+\frac{1}{2} x^2 \log (x)+\frac{x}{2}-\frac{1}{2} x \log (x)+\frac{1}{2} x \log (\pi )+\frac{1}{2} x \log (2)+\frac{\log (x)}{12} + R(x),$$ where $R(x)\longrightarrow 0$ for $x\to \infty$. Here, $A$ is Glaisher's constant (exact value not important). Inserting this in the binomial sum and simplifying yields: $$x^2 \left(\frac{\log (x)}{2}-2 \log \left(x+\frac{1}{4}\right)+3 \log \left(x+\frac{1}{2}\right)-2 \log \left(x+\frac{3}{4}\right)+\frac{1}{2} \log (x+1)\right)+x \left(-\frac{\log (x)}{2}+\log \left(x+\frac{1}{4}\right)-\log \left(x+\frac{3}{4}\right)+\frac{1}{2} \log (x+1)\right)+\frac{\log (x)}{12}+\frac{1}{24} \log \left(x+\frac{1}{4}\right)-\frac{1}{4} \log \left(x+\frac{1}{2}\right)+\frac{1}{24} \log \left(x+\frac{3}{4}\right)+\frac{1}{12} \log (x+1),$$ which I believe you can again compute the limit of.

Neckverse Herdman
  • 1,746