Let $t >0$ and $x_1,x_2 \in {\mathbb R}$ and consider the following quantity below:
\begin{equation} Z_+^{(0)}(x_1,x_2,t):= \frac{1}{\sqrt{4 \pi t}} \left( \exp(-\frac{(x_2-x_1)^2}{4 t}) - \exp(-\frac{(x_2+x_1)^2}{4 t}) \right) \tag{1} \end{equation}
By the method of images(see equation (20) page 4 in 1), the quantity above, represents the probability density for a Brownian motion started at $x_1$ at time zero to hit $x_2$ at time $t$ given that the trajectory is non-negative (absorbing boundary conditions at the x-axis). Now, by using the formula $\int\limits_0^\infty \exp(-A/\xi^2 - B\cdot \xi^2) d\xi = \sqrt{\pi}/2 \exp(-2 \sqrt{A B})/\sqrt{B} $ for $A,B > 0 $ we can easily give the Laplace transform of the quantity in (1). It reads:
\begin{equation} {\tilde Z}_+^{(0)}(x_1,x_2,s) = \frac{1}{2\sqrt{s}} \left( e^{-\sqrt{s} |x_1-x_2|} - e^{-\sqrt{s} (x_1+x_2)} \right) \tag{1a} \end{equation}
Now let $s, \tau >0$ and consider the following integral(see equation (46) page 6 in 1):
\begin{equation} {\mathfrak f}_{x_1,x_2}^{(s)} (\tau) := \int\limits_\tau^\infty \frac{\exp(-s t)}{t} Z_+^{(0)}(x_1,x_2,t) dt \tag{2} \end{equation}
Now, by expressing the Gaussian terms in (1) by inverse Fourier transforms we can show the following identities:
\begin{eqnarray} {\mathfrak f}_{x_1,x_2}^{(s)} (\tau) &=&\frac{1}{\pi} \int\limits_0^\infty \Gamma(0,(s+k^2)\tau) \left( \cos(k(x_1-x_2)) - \cos(k(x_1+x_2))\right) dk \\ &=&\frac{1}{\pi} \int\limits_0^\infty \frac{2 k e^{-\tau \left(k^2+s\right)} }{k^2+s} \left( \frac{\sin(k(x_1-x_2)}{x_1-x_2} - \frac{\sin(k(x_1+x_2)}{x_1+x_2}\right) dk \\ &=& -\frac{1}{\pi} \int\limits_0^\infty \left( \frac{e^{-\left(\tau \left(k^2+s\right)\right)} \left(2 k^2+\tau \left(4 k^4+4 k^2 s\right)-2 s\right)}{\left(k^2+s\right)^2}\right) \left( \frac{\cos(k(x_1-x_2)}{(x_1-x_2)^2} - \frac{\cos(k(x_1+x_2)}{(x_1+x_2)^2}\right) dk \tag{3} \end{eqnarray} where the last two lines were obtained by integrating by parts once and twice respectively.
In[480]:=
Zp0[x1_, x2_, t_] :=
1/Sqrt[4 Pi t] (Exp[-(x2 - x1)^2/(4 t)] - Exp[-(x2 + x1)^2/(4 t)]);
{x1, x2, s} = RandomReal[{1, 2}, 3, WorkingPrecision -> 50];
\[Tau] = 10^(-6);
SetOptions[NIntegrate, WorkingPrecision -> 15, PrecisionGoal -> 10,
MaxRecursion -> 15];
NIntegrate[Exp[-s t]/t Zp0[x1, x2, t], {t, \[Tau], Infinity}]
2 NIntegrate[
Gamma[0, (s + k^2) \[Tau]] (Cos[k (x1 - x2)] -
Cos[k (x1 + x2)]), {k, 0, Infinity}]/(2 Pi)
-2 NIntegrate[-((2 E^-((k^2 + s) \[Tau]) k)/(
k^2 + s)) (Sin[k (x1 - x2)]/(x1 - x2) - Sin[k (x1 + x2)]/(
x1 + x2)), {k, 0, Infinity}]/(2 Pi)
-2 NIntegrate[(
E^-((k^2 + s) \[Tau]) (2 k^2 -
2 s + (4 k^4 + 4 k^2 s) \[Tau]))/(k^2 +
s)^2 (Cos[k (x1 - x2)]/(x1 - x2)^2 -
Cos[k (x1 + x2)]/(x1 + x2)^2), {k, 0, Infinity}]/(2 Pi)
+2 NIntegrate[-((
4 E^-((k^2 + s) \[Tau]) k (k^2 -
3 s + (k^4 - 2 k^2 s - 3 s^2) \[Tau] + (2 k^6 +
4 k^4 s + 2 k^2 s^2) \[Tau]^2))/(k^2 + s)^3) (Sin[
k (x1 - x2)]/(x1 - x2)^3 - Sin[k (x1 + x2)]/(x1 + x2)^3), {k,
0, Infinity}]/(2 Pi)
+2 NIntegrate[(
4 E^-((k^2 + s) \[Tau]) (3 k^4 - 18 k^2 s +
3 s^2 + (3 k^6 - 15 k^4 s - 15 k^2 s^2 +
3 s^3) \[Tau] + (-12 k^6 s - 24 k^4 s^2 -
12 k^2 s^3) \[Tau]^2 + (4 k^10 + 12 k^8 s +
12 k^6 s^2 + 4 k^4 s^3) \[Tau]^3))/(k^2 +
s)^4 (Cos[k (x1 - x2)]/(x1 - x2)^4 -
Cos[k (x1 + x2)]/(x1 + x2)^4), {k, 0, Infinity}]/(2 Pi)
Out[484]= 2.57551235522698
Out[485]= 2.57551235522713
Out[486]= 2.57551235522698
Out[487]= 2.57551235522698
Out[488]= 2.57551235522698
Out[489]= 2.57551236445117
Now, by using the Cauchy theorem being applied to the the last expression in (3) above we easily see that $f(0) = e^{-\sqrt{s} |x_1-x_2|}/|x_1-x_2| - e^{-\sqrt{s} |x_1+x_2|}/|x_1+x_2|$. As such the value at zero of the function in (2) is finite. It turns out that this function approaches that value very smoothly from the right and in fact all the derivatives of that function at zero vanish. On the other hand if we truncate the upper limit of integration in the right hand side in the top line in (3) then, by using the series expansion $\Gamma(0,\tau) = -\gamma - \log(\tau) + O(\tau)$, we can see that, for every truncation threshold $M$, our function has a logarithmic singularity at the origin. We can see all this in the plot below where I show the truncated $k$-integrals for different threshold values $M=1/2,1,2$ (blue,green and red respectively) along with the improper integral (black) all that as a function of $\tau$. Here you go:
As such all this is in perfect unison with what the paper claims (albeit the notation being used there is a bit confusing).
see equations (46) and (47) in pages 6 and 7 respectively:
In the next step we will be computing the propagator of the fractional Brownian motion (fBM).
First of all we define the action $ {\mathcal S}[x] := 1/2 \int\limits_{[0,t]^2} G(t_1,t_2) \cdot x(t_1) x(t_2) d t_1 dt_2 = {\mathcal S}^{(0)}[x] + (H-1/2)^1 {\mathcal S}^{(1)}[x] + O((H-1/2)^2) $ where $G(t_1,t_2)$ is the functional inverse of the auto-covariance of the fBM. In other words we have $(G^{-1})(t_1,t_2) := t_1^{2 H} + t_2^{2 H} - \left| t_1-t_2 \right|^{2 H}$.
Being braced with this we are ready to define the first order correction to the propagator (compare equation (34) in the paper):
\begin{equation} Z_+^{(1)}\left(x_0,x,t\right):= -\frac{1}{x_0} \int\limits_{x(0)=x_0}^{x(t)=x} {\mathcal D}[x] \cdot {\mathcal S}^{(1)}[x] \cdot e^{-{\mathcal S}^{(0)}[x]} \cdot \Theta[x] \tag{4} \end{equation} Here $\Theta[x]$ is a Heaviside function applied to the whole path $x$. Its purpose is to enforce the path (trajectory) to be non-negative.
Now, we split the quantity in $(4)$ into two terms one being hard and another one rather simple. Here we go:
\begin{eqnarray} &&Z_+^{(1)}\left(x_0,x,t\right)=\\ && \underbrace{\frac{1}{2 x_0} \int\int\limits_{0 \le t_1 \le t_2 \le t} d t_1 dt_2 \cdot \int\limits_{x(0)=x_0}^{x(t)=x} {\mathcal D}[x] \frac{\dot{x(t_1)}\dot{x(t_2)}}{|t_1-t_2|} \cdot e^{-{\mathcal S}^{(0)}[x]} \cdot \Theta[x]}_{Z_+^B\left(x_0,x,t\right)} + \\ && \underbrace{\frac{2}{x_0} \left(1+\log(\tau)\right) \cdot \int\limits_{x(0)=x_0}^{x(t)=x} {\mathcal D}[x] \cdot {\mathcal S}^{(0)}[x] \cdot e^{-{\mathcal S}^{(0)}[x]} \cdot \Theta[x]}_{Z_+^A\left(x_0,x,t\right)} \tag{5} \end{eqnarray} where we used the functional form of the first correction to the action (see equation (30) in the paper).
Now it turns out that the "hard" part of the first order correction, i.e. the $Z_+^B$ quantity, has a simpler form after being Laplace transformed. It reads as follows (compare equation (42) in the paper):
\begin{eqnarray} {\tilde Z}_+^{B}(x_0,x,s) := -\frac{2}{x_0} \int\limits_0^\infty \int\limits_0^\infty {\tilde Z}_+^{(0)}(x_0,x_1,s) {\tilde Z}_+^{(0)}(x_2,x,s) \frac{\partial}{\partial x_1} \frac{\partial}{\partial x_2} \left[ {\mathfrak f}_{x_1,x_2}^{(s)}(\tau) \right] \cdot d x_1 d x_2 \tag{6} \end{eqnarray}
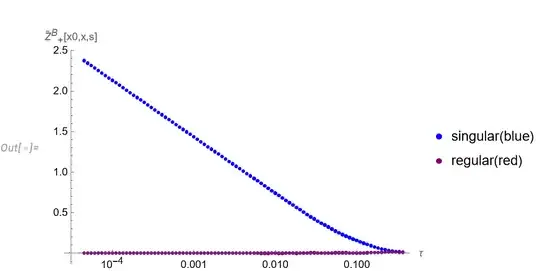
Now, the paper claims (see equation (50) in page 7) that the quantity above has a logarithmic divergence in $\tau$. The objective of this post is to reproduce that equation , using exact calculations (without small-$\tau$ approximations), and then establish once and for all whether that quantity does have or does not have that logarithmic divergence (in what sense does it have that divergence). This is the first objective o this post.
The second objective is to verify that the first order correction to the propagator, as in $(4)$ above, does not depend on the cut-off $\tau$. This is absolutely necessary to verify because otherwise it wouldn't be possible to take the limit of the cut-off going to zero.
1: Kay Joerg Wiese, Perturbation Theory for Fractional Brownian Motion in Presence of Absorbing Boundaries, arXiv 1011.4807
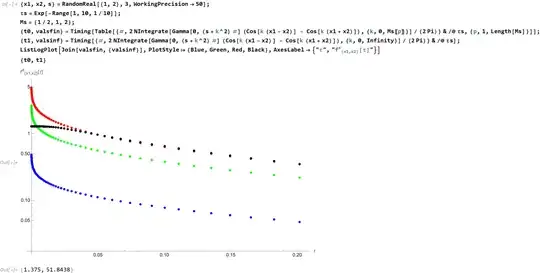
$\tau$." />
$s$-domain numerically and analytically." />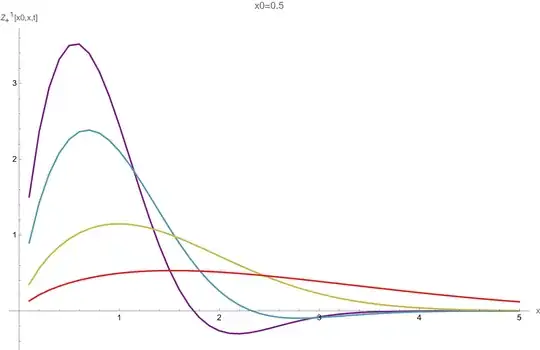
$t=1/3,1/2,1,2$ (from violet to red respectively)." />
$(VIb)$. " />
$(II)$." />