Mellin Transform of $\frac{1}{x^4+1}$ for $0

Question

While reviewing contour integration, I found the following question: prove that if $0<s<4$ then $$ \int_0^\infty \frac{x^{s-1}}{x^4+1}dx=\frac{\pi}{8\sin(\frac{\pi s}{4})} $$ This seemed like an easy enough integral to evaluate using residues. I considered the following contour $\gamma$

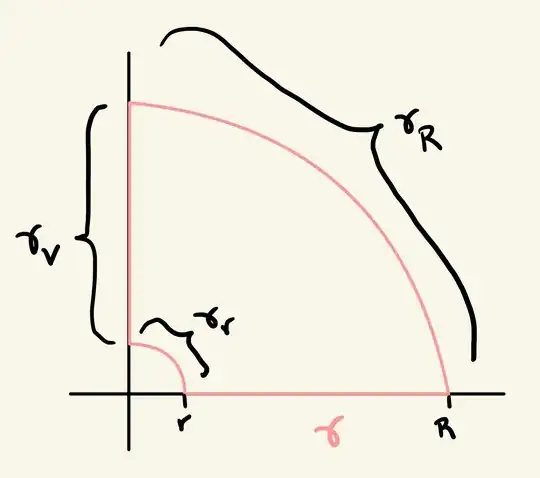$\gamma$ in pink with the segments $\gamma_r$, $\gamma_R$, and $\gamma_v$ referred to below." />

Now, I can estimate that for $r<1$ and $R>1$ we have (by the ML inequality) that $$ \left|\int_{\gamma_r}f(z) dz\right| \leq \frac{r^s}{1-r^4}, \quad \left|\int_{\gamma_R}f(z) dz\right| \leq \frac{R^s}{R^4-1} $$ hence $$ \lim_{r\rightarrow 0}\int_{\gamma_r}f(z) dz=\lim_{R\rightarrow \infty}\int_{\gamma_R}f(z) dz= 0 $$ Moreover, by parameterizing the integral we can see that $$ \int_{\gamma_v}f(z)dz = ie^{\frac{\pi is}{2}} \int_0^\infty f(x)dx $$ Then the residue theorem implies that $$ \int_\gamma f(z) dz =2\pi i \operatorname{Res}(f,e^{\frac{\pi i}{4}}) = -\frac{\pi i}{2}e^{\frac{\pi is}{4}} $$ and putting this together with the above reasoning we see that $$ \int_0^\infty \frac{x^{s-1}}{x^4+1}dx=-\frac{\pi i}{2(1+ie^{\frac{\pi is}{2}})}e^{\frac{\pi is}{4}} $$ It seems that all is left is some algebraic manipulation, but I cannot seem to work it out myself. Any hint would be much appreciated.