1

Why is the inclusion-exclusion principle for three sets $|A\cup B\cup C|=|A|+|B|+|C|−(|A\cap B|+|A\cap C|+|B\cap C|)+|A\cap B\cap C|$? In particular, why it is not $|A\cup B\cup C|=|A|+|B|+|C|−(|A\cap B|+|A\cap C|+|B\cap C|)+2|A\cap B\cap C|$?

If we subtract $|A\cap B|+|A\cap C|+|B\cap C|$, surely we have subtracted $|A\cap B\cap C|$ twice, not just once?

Asaf Karagila
  • 405,794
Juan Millas
  • 21
  • 1
    Welcome to MSE. For some basic information about writing mathematics at this site see, e.g., basic help on mathjax notation, mathjax tutorial and quick reference, main meta site math tutorial and equation editing how-to. – José Carlos Santos Aug 11 '24 at 17:47
  • Why not check it with some examples? Just pick some sets $A,B,C$ with non-trivial joint intersection and see which formula works. Try $A={1,2,3}$, $B={2,3,4}$ and $C={3,4,5}$ for example. Or, more simple, take all three sets equal to ${1}$. – lulu Aug 11 '24 at 17:49
  • 5
    Let $x \in A \cap B \cap C$. Then $|A|+|B|+|C|$ counts $x$ three times, the two-way intersections un-count $x$ three times, so we need to put one copy of $x$ back in at the end. – Eric Towers Aug 11 '24 at 17:53
  • Yeah I understand now it Eric, (a'+a+x+b)+(b'+b+x+c)+(a+x+c+c')-(a-x)-(b-x)-(c-x)+x... total x is one time x. Thanks. – Juan Millas Aug 11 '24 at 18:04
  • 1
    This SHOULD be intuitive and it should need not grounding in mathematics that that it should be what it is and not what you think it is. $A$ contains one iteration of $A\cap B\cap C$ and $B$ contains another and $C$ a third. That is $3$ interations (when there should be only one). $|A\cap B|$ also contains one iteration, and $|A\cap C|$ another and $|B\cap C|$ a third. So when we subtract them we have $3-3 = 0$ iterations. But we need one so we have to add it back. – fleablood Aug 11 '24 at 18:09
  • 1
    See this article for an introduction to Inclusion-Exclusion. Then, see this answer for an explanation of and justification for the Inclusion-Exclusion formula. – user2661923 Aug 11 '24 at 21:22

3 Answers3

3

If you are satisfied with the inclusion-exclusion formula for two sets another possibility is to look at $A\cup B\cup C$ as $(A\cup B)\cup C$ (union of two sets). Then $$ |(A\cup B)\cup C|=|A\cup B|+|C|-|(A\cup B)\cap C|. $$ Distributing $\cup$ over $\cap$ the last formula becomes $$ |A\cup B\cup C|=|A\cup B|+|C|-|(A\cap C)\cup(B\cap C|. $$ Applying again the inclusion-exclusion formula for two sets in the RHS we get $$ |A\cup B\cup C|=|A|+|B|-|A\cap B|+|C|-(|(A\cap C|+|B\cap C|-|A\cap C\cap B \cap C|). $$ Now note that $A\cap C\cap B \cap C=A\cap B \cap C$ and after reordering the terms you get the formula $$ |A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B \cap C|). $$

Andrea Mori
  • 28,458
2

If $x$ belongs to all three sets, then the $|A|+|B|+|C|$ part of the formula counts $x$ three times. And, since $x$ also belongs to $A\cap B$, $A\cap C$ and $B\cap C$, the $-(|A\cap B|+|A\cap C|+|B\cap C|)$ part of the formula would uncount it three times. Therefore, since $x\in A\cap B\cap C$, there is now way the formula$$|A|+|B|+|C|-(|A\cap B|+|A\cap C|+|B\cap C|)+2|A\cap B\cap C|$$will work (it will count $x$ twice). But the formula$$|A|+|B|+|C|-(|A\cap B|+|A\cap C|+|B\cap C|)+|A\cap B\cap C|$$still has a fighting chance…

Another User
  • 5,585
0

That's because $|A|+|B|+|C|$ already counts the $|A\cap B\cap C|$ $3$ times here, isn't it?

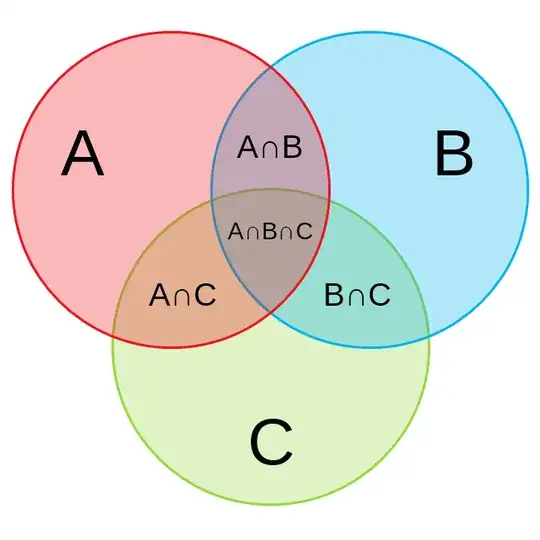
A Venn Diagram for 3 Sets

Also, this principle works for all numbers of finite sets, that is, for $n\in\mathbb{N}$ number of sets. And it has a generalized formula:

Given $X_1,\cdots, X_m $ are finite sets, $$|\bigcup_{i=1}^m X_i|=\sum_{1\le i_1\le m}|X_{i_1}|-\sum_{1\le i_1< i_2\le m}|X_{i_1}\cap X_{i_2}|+\sum_{1\le i_1<i_2<i_3\le m}|X_{i_1}\cap X_{i_2}\cap X_{i_3}|-\cdots + (-1)^{m-1} |X_1\cap \cdots \cap X_m|$$

In which for intersection of odd numbers of sets, to count the total size, we decrease the size of these sets, and add those intersections of even numbers of sets.

A proof can be done by second form of induction:

Let this statement be $P$

$P(1)$ holds as $|X_1|=1\cdot |X_1|$

Suppose $P(n)$, for natural number $n\le k$ holds, $k\ge 2$ we now prove $P(k+1)$ also holds.

Now $$\bigcup_{i=1}^{k+1} X_i=X_{k+1}\cup \bigcup_{i=1}^{k} X_i$$

We apply $|A\cup B|=|A|+|B|-|A\cap B|$ to this, which is statement $P(2)$, holds as $k\ge 2$

And we will naturally find that $P(k+1)$ also holds!

Liyang Meng
  • 693