Relation between row and collumn sums for spanning trees of square grids and (0,1)-matrices

Question

I was counting the horizontal and vertical edges in spanning trees of a $n \times n$ grid graph. For example for the following spanning tree of the $3\times 3$ grid:

we have (2,2) for the horizontal edges and (3,1) for the vertical edges. I counted how many variations of [(2,2),(3,1)] could appear (counted with ordering) for $n=2,3,4,5$ and found that this corresponds to A297077 ( https://oeis.org/A297077 ) which is both the number of distinct row and column sums for $(n-1)\times (n-1)$ - $(0, 1)$-matrices and the number of spanning forests of the complete bipartite graph $K_{(n-1),(n-1)}$ (as shown in Spanning forests of bipartite graphs and distinct row/column sums of binary matrices ). I am most interested in the former.

Is there a mapping between a spanning tree and a $(0,1)$-matrix?

---

(My attempt was to first look at the latter. I tried to look at the grid as a checker-board where the nodes are the corners and a small square of 4 nodes form a tile. The tiles can either be separated by an edge or not. In this way, one obtains a $(n-1)\times(n-1)$ forest where the tiles are nodes but there seem to be multiple ways to obtain the same forest, e.g. in the picture switch the edge between (3,2) and (3,3) to an edge between (2,3) and (3,3). On the other hand not all bipartite forests can be obtained if $n\geq 4$, so this doesn't really help much. The center tiles cannot be separated from the rest.)

Another example: in the case of $n=2$ we have the $\cap$- and $\cup$-shape that give [(1),(2)] and the $\subset$- and $\supset$-shape that give [(2),(1)]. On the other hand the possible $(0,1)$-matrices are $[0]$ which gives $[(0),(0)]$ as row and column sum and $[1]$ with $[(1),(1)]$.

Answer 1

The mapping is between the row sums and the column sums. If you have a $(0,1)$-matrix with row sums $(r_1,...,r_{n-1})$ and column sums $(c_1,...,c_{n-1})$ then there is a spanning tree with row sums $(1+r_1,...,1+r_{n-1})$ and column sums $(n-c_1,...,n-c_{n-1})$.

The interpretation for every one and zero on a tile is that a one is a vertical arrow and a zero a horizontal arrow that points to the next tile on the path of tiles to an open edge on the border of the grid. So zeros open a vertical edge and ones open a horizontal edge. It doesn't matter where you place the edges exactly.

In the example this would be 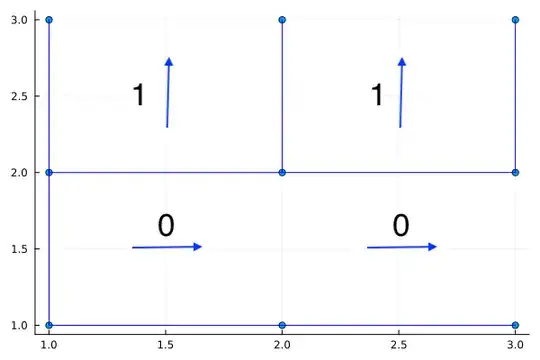, but note that the same matrix would be found if we swapped the edge [(1,2),(2,2)] for [(1,3),(2,3)] for example. The direction of the arrow would change then from up to down but not the number of horizontal edges in that column.

---

For a more formal version and slightly more general version, let us start with some notation. Contrary to the above I will here use the first ordinate for the vertical direction and the second ordinate for the horizontal direction. (Don't blame me, blame the person that thought it was logical to first do rows and then columns in notation of matrices.)

For the $m \times n$ grid graph let us use coordinates $\{(1,1),...,(1,n),(2,1),...,(2,n),...,(m,n)\}$ to denote the nodes so that the edges are all of the form $[(k,\ell),(k+1,\ell)]$ or $[(k,\ell),(k,\ell+1)]$.

Let $(v_1,...,v_{m-1})$ be called the vertical edge sequence of spanning tree of a grid graph if the spanning tree has $v_k$ edges of the form $[(k,\ell),(k+1,\ell)]$ for each $k \in \{1,...,m-1\}$ and similarly $(h_1,...,h_{n-1})$ be called the horizontal edge sequence of such spanning tree if there are $h_{\ell}$ edges of the form $[(k,\ell),(k,\ell+1)]$ for each $\ell \in \{1,...,n-1\}$.

Any $m\times n$ grid graph has a dual graph that is special in the sense that it is a $(m-1)\times (n-1)$ grid graph but with one added node that is connected to all nodes on the 'outside' of the grid; that is the nodes that have less than four neighbours in the grid. So, for the dual we talk about its grid for its grid part and its root for its outside node. As explained on wikipedia: "each spanning tree of G is complementary to a spanning tree of the dual graph, and vice versa".

A map from the nodes of a grid graph can be seen as a matrix since we used integer coordinates for each of them. In the next lemma we will use a map to $0$ or $1$, which corresponds to a binary matrix.

Theorem 1 Consider any $m\times n$ grid graph $G$ with vertical edge sequence $(v_1,...,v_{m-1})$ an horizontal edge sequence $(h_1,...,h_{n-1})$ and its dual graph with grid $H$. Then there is a map from the nodes of $H$ to $\{0,1\}$ so that the associated matrix has row sums $(v_1-1,...,v_{m-1}-1)$ and column sums $(m-h_1,...,m-h_{n-1})$.

Proof of Theorem 1 The construction we need is that we map a node to $0$ if the next edge on the path to root is horizontal and $1$ if it is vertical. If the next node is root, we are at a border and it is still possible to define horizontal and vertical in this context because it can only leave the corresponding face of the original grid graph in one of these direction.

To prove that the counting matches, we must notice that every vertical edge of the dual graph cuts away exactly one edge in the original graph. The original grid graph had vertical edge count $(n,...,n)$ and horizontal edge count $(m,...,m)$. For the vertical edge count we remove the number of $0$'s in that row which is $n-1-r_k$ and for the horizontal edge count we remove the number of $1$'s in that column, which is $c_\ell$. $\square$

Conjecture 2 Consider any two finite integer sequences of $(r_1,...,r_m)$ and $(c_1,...,c_n)$. There is a binary matrix $A \in \{0,1\}^{m \times n}$ so that $r_k$ is the row sum of the $k$'th row and $c_k$ is the column sum of the $k$'th column if and only if there is a spanning tree of the $(m+1)\times (n+1)$ grid graph that has $(1+r_1,...,1+r_m)$ as vertical edge sequence and $(m+1-c_1,...,m+1-c_n)$ as horizontal edge sequence.