2

The following question is from Oxford's Math Admissions Test, 2019 (Q1E):

The graph of $\sin y − \sin x = \cos^2 x − \cos^2 y$ (a) is empty (b) is non-empty but includes no straight lines (c) includes precisely one straight line (d) includes precisely two straight lines (e) includes infinitely many straight lines

The answer is e. When trying to solve graphically on Desmos, I found this: 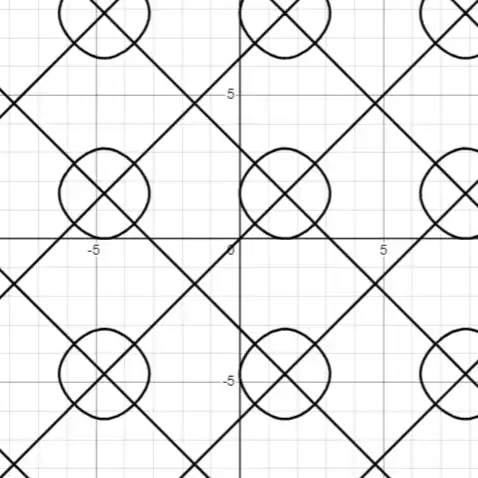Graph of <span class=$\sin y − \sin x = \cos^2 x − \cos^2 y$" />

The criss-crossing lines are of course the intersect of the solution sets $\sin y - \sin x = 0$ and $\cos^2 x − \cos^2 y = 0$. But how do the weird shapes come by? They are not circles, as evident when compared to the circle $\left(x-\frac{\pi}{2}\right)^{2}+\left(y-\frac{\pi}{2}\right)^{2}=\frac{\pi^{2}}{4}$.

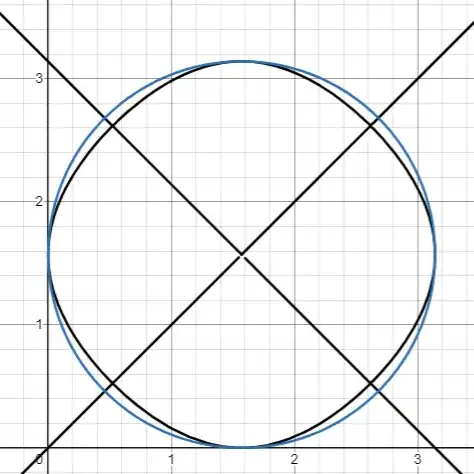Ellipses in the graph of <span class=$\sin y − \sin x = \cos^2 x − \cos^2 y$ compared to a " />

ultralegend5385
  • 10,106
  • https://math.stackexchange.com/questions/175143/prove-sinab-sina-b-sin2a-sin2b – lab bhattacharjee Aug 05 '24 at 09:52
  • Upon further inspection, I found that they are the solutions to the equation $siny + sinx = 1$. I have never seen this before, can someone point me to somewhere where I can learn more about this? Also, why can't I get this subset of solutions by finding the intersect of the solution sets $siny−sinx=0$ and $cos2x−cos2y=0$? –  Aug 05 '24 at 09:57
  • 1
    @SzeYoongLow $\sin y + \sin x = 1$ and $\sin y−\sin x=0$ simultaneously would imply $\sin y=\sin x= \frac12$ and these are where the straight lines and curved shapes intersect. – Henry Aug 05 '24 at 10:04
  • @Henry. What could be the equation of the weird shapes ? – Claude Leibovici Aug 05 '24 at 10:36
  • @ClaudeLeibovici As both Sze Yoong Low and heropup have said: $\sin y + \sin x = 1$ – Henry Aug 05 '24 at 10:42

1 Answers1

2

Note that $$\begin{align} \sin y - \sin x & = \cos^2 x - \cos^2 y \\ &= (1 - \sin^2 x) - (1 - \sin^2 y) \\ &= \sin^2 y - \sin^2 x \\ &= (\sin y - \sin x)(\sin y + \sin x). \end{align}$$ So whenever $\sin y \ne \sin x$, $$1 = \sin y + \sin x.$$

Regarding your question as to why this does not arise from solving the simultaneous conditions $$\begin{cases} \sin y - \sin x = 0 \\ \cos^2 x - \cos^2 y = 0, \end{cases}$$ the reason is because there is no requirement that each side of the given equation must equal zero. For instance, you could have $\sin y - \sin x = \frac{1}{2} = \cos^2 x - \cos^2 y$.

heropup
  • 143,828
  • Wow! This is enlightening. Equating both sides to a real number $n\in\mathbb{R}, -1\le n \le 1$ yields a set of solutions; the union of all these sets forms the weird shape. Here's the Desmos graph, where you can visualize it. –  Aug 05 '24 at 10:38
  • So the equation simplifies to $(\sin y-\sin x)(\sin y+\sin x-1)=0$, and its graph is therefore just the union of the graphs for $\sin y-\sin x=0$ and $\sin y+\sin x-1=0$. The former is the straight lines, the latter is the loops. – Jaap Scherphuis Aug 05 '24 at 12:42