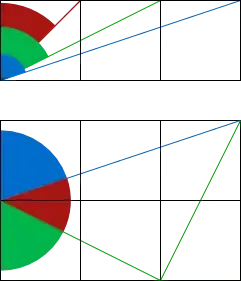
I recently found a fun proof of $\arctan (1)+\arctan (2)+\arctan (3)=\pi$ from this answer
It's an "Aha" moment for me as I realized the proof's simplicity, still I was surprised by the result summing up to $\pi$.
What are some results that are straightforward to understand but have outcomes that are unexpectedly profound or interesting?