1

In the book of Vakil, the Foundation Of Algebraic Geometry, there is an exercise (19.4.A) that I can't do and I'd like to have some help.

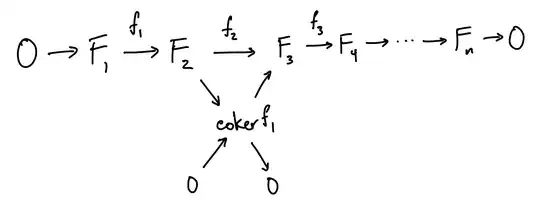
The exercise is the following : We take a projective $k$-scheme $X$ and an exact sequence of coherent sheaves $\require{AMScd} \begin{CD} 0 @>>> \mathscr{F}_1 @>>> \cdots @>>> \mathscr{F}_n @>>> 0 \end{CD}$ We have to show that the alternated sum of the Euler characteristics of the sheaves is 0.

It is easy to do it when $n=3$ but when the exact sequence is long, it is more difficult. Vakil says to consider first the case $X=\operatorname{Spec}(k)$ but I don't manage to do it.

Geomat
  • 21

1 Answers1

2

Once you can do it for $n \leq 3$ you're done by induction!

For the inductive step, you can split a longer exact sequence into two smaller exact sequences:

$$\begin{array}{ccccccccccccccc} 0&\longrightarrow&F_1&\overset{f_1}{\longrightarrow}&F_2&\overset{f_2}{\longrightarrow}&F_3&\overset{f_3}{\longrightarrow}&F_4&\cdots \rightarrow&F_n&\rightarrow&0\\ &&&& \ \searrow&&\nearrow \ \ &&&&&&\\ &&&&& \operatorname{coker} f_1 &&&&&\\ &&&& \ \ \ \ \nearrow&&\searrow \ \ &&&& \\ &&&&0 & & \ \ 0 \end{array}$$

enter image description here

In the above, $0 \to F_1 \to F_2 \to \operatorname{coker} f_1 \to 0$ is exact, and so is $0 \to \operatorname{coker} f_1 \to F_3 \to F_4 \to \dots \to F_n \to 0$. By inductive hypothesis, you get

$$\chi(F_1) - \chi(F_2) + \chi(\operatorname{coker} f_1) = 0$$

and

$$\chi(\operatorname{coker} f_1) - \chi(F_3) + \chi(F_4) - \dots \pm \chi(F_n) = 0.$$

Now subtract the second equation from the first :)

Jean Marie
  • 88,997
diracdeltafunk
  • 16,589
  • 1
    I have taken the liberty to write your exact sequences under a Mathjax form... It is not the nicest form (see for example the way the asker uses AMScd library) – Jean Marie Aug 01 '24 at 17:17
  • Thanks a lot ! However, I don't understand why the author proposes to do it first for X=Spec(k). – Geomat Aug 01 '24 at 20:40