A doubt on polar coordinates in the plane

Question

I'm here to ask a really stupid question just to be sure of its answer. My professor gave us an exercise where we have to determine the Lagrangian of a system that is formed by a circular ring of mass $M$ and radius $R$ which is placed in the $(x,z)$ plane. In this plane, it rotates around one of his point $O$ fixed in the origin of the axes. Also, there is a particle $P$ of mass $m$ that moves on this ring-like object without friction.

The Lagrangian has to be written in terms of $\theta$, $\phi$, $\dot{\theta},\dot{\phi}$ where $\theta$ is the angle formed by the segment that connects $O$ with the center $C$ of the ring guide with the $z$ axes and $\phi$ is the angle formed by the segment that connects the position of the particle $P$ with the center of the ring guide $C$ and the $z$ axes.

I have no problem in understanding how to write the Lagrangian itself, but I'm more confused on how the professor wrote the solution for this problem. He stated that the coordinates of the center $C$ of the guide can be written as: $$ \begin{cases} x= R\sin \theta\\ z=-R \cos\theta \end{cases} $$ where I would have written $z = R \sin\left(\frac{\pi}{2}-\theta\right)=R \cos\theta$, hence the position of the point $P$ should be expressed as: $$ \begin{cases} x= R(\sin \theta + \sin\phi)\\ z=R (\cos\theta+\cos \phi) \end{cases} $$ and not as my professor did:

$$ \begin{cases} x= R(\sin \theta + \sin\phi)\\ z=-R (\cos\theta+\cos \phi) \end{cases} $$

I'll add an image of the problem so that it is easier to visualize the system. This is not official, it is how I understood it. 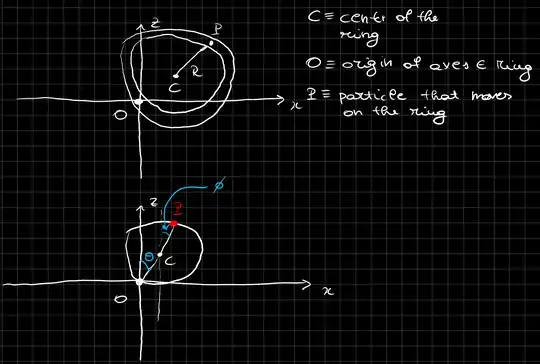Keep in mind that the ring guide can rotate around the origin $O$, where $O$ is always a point on the guide, so $\theta$ is not fixed.

Sorry for my really bad drawing ability and thanks a lot in advance for your help!

Answer 1

Your professor uses $z$, traditionally the upwards coordinate in a gravitational field in $\mathbb R^3$.

If he is writing $z=-R $ for $\theta =0, \phi=0$ he wants the equilibrium position to be in the minimum of the potential energy, that is free for gauging it by a constant, deliberately setting it to zero somewhere in space.

Setting the potential energy to zero in its minimum, considerably simplifies the algebra with a positive total energy involving terms like $$V=R(1-\cos \theta) = 2 R \ \sin^2\left(\frac{\theta}{2}\right)$$

With kinetic energy $$T=\frac{1}{2} \ R^2 \ \dot \theta^2$$

you see without any calculus involved, that for small $\theta$ you have a harmoic oscillator.

$$L= \frac{1}{2}\left( \ R^2 \ \dot \theta^2 - R^2 \theta^2 \right)$$

Your attempt to put the zero of the angular coordinate on top is destructive: For oscillatory motions the point never passes the top hovering around $\theta =\pm \pi ?$. (Ptolemaios failure not to put the sun in the center as Aristarch had recommended)

But you can use it for large energy, resulting in circular motion, with the algebra of elliptic integrals and Jocobi elliptic functions describing non-uniform periodic motions on a circle.