Find the lengths of the semi-axes of the elliptical conic section resulting from the intersection of a plane with a right circular cone

Question

Given a right circular cone, with semi-vertical angle $\theta$ with its vertex at the origin, and its axis along the $z$ axis, and the plane $ n \cdot (r - r_0) = 0 $ where $r_0 = (0,0,z_0)$ and $n = (- \sin \phi, 0, \cos \phi) $, such that $\phi \lt \dfrac{\pi}{2} - \theta$. Find the lengths of the semi-major and semi-minor axes of the ellipse of the intersection between the right circular cone and the plane.

My Attempt:

My attempt is summarized in my answer below.

Alternative solutions are appreciated.

Answer 1

Another take on the geometric solution:

Looking at the configuration "from the side", I'll write $C$ and $P$ for the angles made by the cone and plane with "the horizontal". (So, $C=90^\circ-\theta$ and $P=\phi$ in OP's notation.) Let $O$ be the vertex of the cone, and let the plane meet its axis at $H$ (with $|OH|=h$, aka $z_0$ in OP's notation) and the "edges" of the cone at $U$ and $V$.

Then $UV$ is the ellipse's major axis (traditionally of length $2a$). We calculate that value in terms of $C$, $P$, and $h$ by invoking the Law of Sines in $\triangle HOU$ and $\triangle HOV$:

$$\begin{align} 2a = |HU|+|HV| &=\frac{h\sin\angle HOU}{\sin\angle OUH}+\frac{h\sin\angle HOV}{\sin\angle OVH}=\frac{h\cos C}{\sin(C+P)}+\frac{h\cos C}{\sin(C-P)} \\[6pt] \to \qquad a &= \frac{h\sin2C\cos P}{2\sin(C+P)\sin(C-P)} \tag1 \end{align}$$ This is equivalent to OP's result.

To calculate the minor axis, I'll reference a result worth knowing in its own right (and proven in this ancient answer of mine):

The eccentricity $e$ of a conic determined by "cone angle" $C$ and "plane angle" $P$ is given by $$e = \frac{\sin P}{\sin C} \tag2$$

From $(1)$ and $(2)$, we can calculate the conic's minor radius, $b$, via $$\begin{align} b &= a \sqrt{1-e^2} = \frac{2h\sin C\cos C\cos P}{2\sin(C+P)\sin(C-P)}\cdot \frac{\sqrt{\sin^2C-\sin^2P}}{\sin C} \\[6pt] &=\frac{h\cos C\cos P}{\sqrt{\sin(C+P)\sin(C-P)}} \tag3 \end{align}$$ This, too, is equivalent OP's result.

Notes:

• When $P=0$, we have $a=b=h\cot C$ and $e=0$. The conic is a circle.
• When $P<C$, we have $e<1$, as appropriate for an ellipse.
• When $P=C$, we have $a=b=\infty$ and $e=1$, which is consistent with the fact that the conic corresponding to this situation is a parabola.
• When $P>C$, the conic is a hyperbola. $(2)$ calculates the eccentricity $e>1$ as-is. $(1)$ and $(2)$ also still give the transverse and conjugate radii, provided we take the absolute value of $\sin(C-P)$ (or write it as $\sin(P-C)$).

---

Personal Note. Back in the day, my Pre-Calculus teacher let me do exactly this exploration (and a bit more) as a kind of mini research project.

While the other students were summarizing biographies of famous mathematicians or compiling lists of "When will we use this?"s, I was set loose to independently (re-)discover new(-to-me) geometric facts.

Along the way, I invented notation ("cross-case" letters, for some reason), coined terminology ("selene" and "heliix", for the point and line where the cutting plane met the cone axis and horizontal plane, respectively (I had a bit of a fascination with Greek mythology)), and simply had a blast experiencing mathematics as a creative art.

This is the very topic that flipped my mathematician switch to the "on" position. It's nice to revisit it from time to time. :)

Answer 2

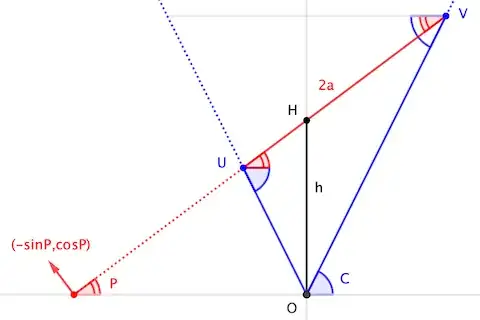
The equation of the right circular cone using vector-matrix notation is

$ r^T Q r = 0 \tag{1} $

where

$ r = [x,y,z]^T $

and

$Q = \begin{bmatrix} \cos^2 \theta && 0 && 0 \\ 0 && \cos^2 \theta && 0 \\ 0 && 0 && - \sin^2 \theta \end{bmatrix} $

The plane can be written in explicit form as

$ r = r_0 + V u \tag{2}$

where

$ V = \begin{bmatrix} \cos \phi && 0 \\ 0 && 1 \\ \sin \phi && 0 \end{bmatrix} $

and $ u = [u_1, u_2]^T $

Substituting $(2)$ into $(1)$ gives

$ (r_0 + V u)^T Q (r_0 + V u) = 0 $

Expanding,

$ u^T V^T Q V u + 2 u^T V^T Q r_0 + r_0^T Q r_0 = 0 \tag{3} $

Evaluating the above matrices, we have

$ V^T Q = \begin{bmatrix} \cos \phi \cos^2 \theta && 0 && - \sin \phi \sin^2 \theta \\ 0 && \cos^2 \theta && 0 \end{bmatrix}$

$V^T Q V = \begin{bmatrix} \cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta && 0 \\ 0 && \cos^2 \theta \end{bmatrix} \tag{4}$

$ V^T Q r_0 = z_0 \begin{bmatrix} - \sin \phi \sin^2 \theta \\ 0 \end{bmatrix} $

$ r_0^T Q r_0 = - z_0^2 \sin^2 \theta $

Now define $ u_0 = - \dfrac{1}{2} (V^T Q V)^{-1} V^T Q r_0 $ to be the center of the conic.

Then

$u_0 = - z_0 \begin{bmatrix} \dfrac{1}{\cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta} && 0 \\ 0 && \dfrac{1}{\cos^2 \theta} \end{bmatrix} \begin{bmatrix} - \sin \phi \sin^2 \theta \\ 0 \end{bmatrix} = \begin{bmatrix} \dfrac{ z_0 \sin \phi \sin^2 \theta }{\cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta} \\ 0 \end{bmatrix}$

Now, equation $(3)$ becomes

$ (u - u_0)^T (V^T Q V) (u - u_0) = - r_0^T Q r_0 + u_0^T (V^T Q V) u_0 $

We now have

$ u_0^T (V^T Q V) u_0 = \dfrac{ z_0^2 \sin^2 \phi \sin^4 \theta }{\cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta} $

So that

$ - r_0^T Q r_0 + u_0^T (V^T Q V) u_0 = \dfrac{ z_0^2 \cos^2 \phi \cos^2 \theta \sin^2 \theta }{\cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta} \tag{5}$

From $(4), (5)$, it follows that the semi-axes are

$\text{Major Axis:} $

$ a = \dfrac{ z_0 \cos \phi \cos \theta \sin \theta }{\cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta} =\dfrac{ z_0 \cos \phi \tan \theta }{ 1 - \sec^2 \theta \sin^2 \phi} $

$\text{Minor Axis:}$

$ b = \dfrac{ z_0 \cos \phi \sin \theta }{\sqrt{ \cos^2 \phi \cos^2 \theta - \sin^2 \phi \sin^2 \theta } } =\dfrac{ z_0 \cos \phi \tan \theta}{ \sqrt{ 1 - \sec^2 \theta \sin^2 \phi} }$