Probability of Seeing "X" % of Balls in "Y" Turns?

Question

Here is a math problem I thought of:

• Set up:

  • Suppose we have integers 1,2,3...99, 100
  • Each integer has an equal probability of being selected

• Game:

  • In round=1, we pick 5 numbers randomly without replacement and then put them back
  • In round=2 we again pick 5 numbers randomly without replacement and then put them back
  • We do this until round = 100

I wrote an R program to simulate this situation:

 round   numbers_picked         cumulative_unique_numbers_seen     percent_of_new_numbers
     1  31, 79, 51, 14, 67                              5                    100
     2  42, 50, 43, 14, 25                              9                     80
     3  90, 91, 69, 99, 57                             14                    100
     4   92, 9, 93, 72, 26                             19                    100
     5    7, 42, 9, 83, 36                             22                     60
     6  78, 81, 43, 76, 15                             26                     80
     7    32, 7, 9, 41, 74                             29                     60
     8   23, 27, 60, 53, 7                             33                     80
     9  53, 27, 96, 38, 89                             36                     60
    10  34, 93, 69, 72, 76                             37                     20
    11  63, 13, 82, 97, 91                             41                     80
    12  25, 38, 21, 79, 41                             42                     20
    13  47, 90, 60, 95, 16                             45                     60
    14   94, 6, 72, 86, 97                             48                     60
    15  39, 31, 81, 50, 34                             49                     20

I am wondering if there is some probability distribution that can be used to answer the following question:

• Question 1: Suppose we are currently at round = n and we have seen "m" unique numbers. If we know that there are 100 total numbers - what is the probability we will have seen 99% of all numbers by round = k? (k>n)
• Question 2: Suppose we are currently at round = n and we have seen "m" unique numbers. If we DO NOT know that there are 100 total numbers - what is the probability we will have seen 99% of all numbers by round = k? (k>n)

For Question 1, I found out that this is very similar to the Coupon Collector Problem (https://en.wikipedia.org/wiki/Coupon_collector%27s_problem) - but I am not sure how to adapt the answer given in terms of probabilities (given some initial conditions). Only the general expectation and variance are provided. I.e. it tells you how many draws are needed to see all coupons and the variance for the number of draws .... but it doesn't tell you that assuming you have seen n/m coupons in j rounds, what is the probability of seeing (n+k)/m coupons in j+x rounds?

For Question 2, I am not sure if these types of problems can be answered when we don't know the total amount of numbers. I thought perhaps something could be done where we observe if the number of unique coupons seen in each round stabilize towards 0 - heuristically indicating we have seen more and more coupons with higher probabilities?

Can someone please help me answer these? Can we use PGF's? https://en.m.wikipedia.org/wiki/Probability-generating_function

Answer 1

Let's define some nice variables.

Be $X$ the number of balls at the start, and $q$ the number of balls you draw in a given round.

Be $n$ the number of found balls at the start of round k, and $i_{k, p}$ the number of previously unknown numbers drawn during the p first draws of round k.

Be $B_{k, p}$ the ball drawn in the p-th position in round k.

$P(B_{k, p}\hspace{.1cm}is\hspace{.1cm}unseen) = \frac {n-(p-1-i_{k, p-1})}{X - p+1}$

$P(B_{k, p}\hspace{.1cm}is\hspace{.1cm}seen) = \frac {X - n +p-1-i_{k, p-1}}{X - p+1}$ the complement of the above line

$P(i_{k, q} = 0) = \prod_{a=0}^{q}\frac{n-b}{X} = \frac{n!(X-q)!}{X!(n-q)!}$ (first draw, the box is split $n$ seen and $X-n$ unseen ; each draw takes out one seen, reducing the number of seen balls we can draw by one)

$P(i_{k, q} = q) = \prod_{a=0}^{q}\frac{X-n-b}{X} = \frac{(X-n)!(X-q)!}{X!(X-n-q)!}$ through a similar argument (except this time we want only unseen balls)

If you want to know, the factor $\frac{(X-q)!}{X!}$ popping everywhere in your case ($X=100,\hspace{.1cm}q=5$) is roughly 1 in 9 billion

$$ P(i_{k, q} = 1) = \sum_{a=0}^{q-1} \frac{X-n+a}{X-a}\prod_{b=0, b!=a}^{q-1}\frac{n-b}{X-b}$$

$$P(i_{k, q} = 1) = \sum_{a=0}^{q-1} \frac{(X-n+a)}{(n-a)}\prod_{b=0}^{q-1}\frac{n-b}{X-b} $$

(multiplying the product by the term for b=a, $\frac{n-a}{X-a}$ and dividing the expression by this same factor to get a cleaner product)

$$P(i_{k, q} = 1) = \sum_{a=0}^{q-1} \frac{(X-n+a)}{(n-a)}\frac{(n)!(X-q)!}{(n-q)!(X)!}$$

Note that $q<n$ can happen only on round 1, which consists of drawing only new numbers, so I'm not too worried about having $n>q$. If round 1 were composed of less draws than subsequent rounds, care should be exercised.

$$P(i_{k, q} = 1) = \frac{(n)!(X-q)!}{(n-q)!(X)!} \sum_{a=0}^{q-1} \frac{(X-n+a)}{(n-a)}$$

Wolfram Alpha tells me this sum looks like

$$(X-n)(H_n - H_{n-q}) + n*(\digamma{(1-n)}-\digamma{(q-n)}) -q + 1$$where F is digamma

End of reasoning, everything becomes a WORSE mess after. I'm not fluent enough in laTEX for this

Crunching numbers for $P(i_{k, q} = 0)$ with X=100 and q=5, I find that you pass probability 1/2 of not finding any new number on a given round, once n passes 88 ; even probability 1/10 of not finding anything new waits until a nice n=69. The more you have balls in your initial box, the later this will happen relatively, I wager, due to the factorials everywhere, with $\frac{(X-q)!}{X!}$ coming down faster than $\frac{n!}{(n-q)!}$ grows.

When you don't know the number of balls, and draw only q by q, you can only be relatively certain you have encountered all m balls when the number of balls you have encountered stays identical for at least m/q rounds in a row (probability of getting a new ball when you have all of them except one, is q/n ; I'm rusty on the number of tries you need to do for a 95%confidence interval, but it can't be lower than n/q)

Answer 2

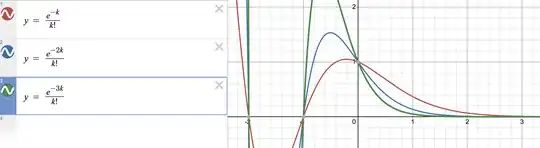
Numerical Analysis - Brute Force (Optional)Numpy

I wrote a program in Python to numerically calculate the expected probability of 99% seen cumulatively. It seems the answer to Question 1 for 99% cumulative for select 5 out of 100 is 181 rounds empirically for 10,000 trials so it's high certainty.

Question 1: Part1 Answer is Round 181 - Round 185

Percentage(Round number) = PGF

Cumulative(Round number) = CDF

PGF and CDF of Rounds taken for 100 total choices and window size 5

Choosing 5 choices every round till all 100 choices are seen
053 rounds: 001 times, Percentage:000.0% Cumulative:00.01%
054 rounds: 003 times, Percentage:000.0% Cumulative:00.04%
055 rounds: 003 times, Percentage:000.0% Cumulative:00.07%
056 rounds: 001 times, Percentage:000.0% Cumulative:00.08%
057 rounds: 005 times, Percentage:000.1% Cumulative:00.13%
058 rounds: 004 times, Percentage:000.0% Cumulative:00.17%
059 rounds: 010 times, Percentage:000.1% Cumulative:00.27%
060 rounds: 010 times, Percentage:000.1% Cumulative:00.37%
061 rounds: 017 times, Percentage:000.2% Cumulative:00.54%
062 rounds: 014 times, Percentage:000.1% Cumulative:00.68%
063 rounds: 022 times, Percentage:000.2% Cumulative:000.9%
064 rounds: 020 times, Percentage:000.2% Cumulative:001.1%
065 rounds: 031 times, Percentage:000.3% Cumulative:01.41%
066 rounds: 035 times, Percentage:000.3% Cumulative:01.76%
067 rounds: 050 times, Percentage:000.5% Cumulative:02.26%
...
072 rounds: 095 times, Percentage:000.9% Cumulative:05.62%
073 rounds: 096 times, Percentage:001.0% Cumulative:06.58%
074 rounds: 109 times, Percentage:001.1% Cumulative:07.67%
075 rounds: 091 times, Percentage:000.9% Cumulative:08.58%
076 rounds: 117 times, Percentage:001.2% Cumulative:09.75%
...
098 rounds: 190 times, Percentage:001.9% Cumulative:47.12%
099 rounds: 154 times, Percentage:001.5% Cumulative:48.66%
100 rounds: 166 times, Percentage:001.7% Cumulative:50.32%
101 rounds: 199 times, Percentage:002.0% Cumulative:52.31%
...
136 rounds: 048 times, Percentage:000.5% Cumulative:90.07%
137 rounds: 052 times, Percentage:000.5% Cumulative:90.59%
138 rounds: 033 times, Percentage:000.3% Cumulative:90.92%
139 rounds: 052 times, Percentage:000.5% Cumulative:91.44%
140 rounds: 055 times, Percentage:000.6% Cumulative:91.99%
141 rounds: 044 times, Percentage:000.4% Cumulative:92.43%
142 rounds: 030 times, Percentage:000.3% Cumulative:92.73%
143 rounds: 036 times, Percentage:000.4% Cumulative:93.09%
144 rounds: 037 times, Percentage:000.4% Cumulative:93.46%
145 rounds: 025 times, Percentage:000.2% Cumulative:93.71%
146 rounds: 029 times, Percentage:000.3% Cumulative:094.0%
147 rounds: 027 times, Percentage:000.3% Cumulative:94.27%
148 rounds: 031 times, Percentage:000.3% Cumulative:94.58%
149 rounds: 033 times, Percentage:000.3% Cumulative:94.91%
150 rounds: 019 times, Percentage:000.2% Cumulative:095.1%
151 rounds: 023 times, Percentage:000.2% Cumulative:95.33%
152 rounds: 026 times, Percentage:000.3% Cumulative:95.59%
153 rounds: 025 times, Percentage:000.2% Cumulative:95.84%
154 rounds: 018 times, Percentage:000.2% Cumulative:96.02%
155 rounds: 013 times, Percentage:000.1% Cumulative:96.15%
156 rounds: 014 times, Percentage:000.1% Cumulative:96.29%
157 rounds: 016 times, Percentage:000.2% Cumulative:96.45%
158 rounds: 021 times, Percentage:000.2% Cumulative:96.66%
159 rounds: 019 times, Percentage:000.2% Cumulative:96.85%
160 rounds: 007 times, Percentage:000.1% Cumulative:96.92%
161 rounds: 021 times, Percentage:000.2% Cumulative:97.13%
162 rounds: 008 times, Percentage:000.1% Cumulative:97.21%
163 rounds: 017 times, Percentage:000.2% Cumulative:97.38%
164 rounds: 017 times, Percentage:000.2% Cumulative:97.55%
165 rounds: 018 times, Percentage:000.2% Cumulative:97.73%
166 rounds: 011 times, Percentage:000.1% Cumulative:97.84%
167 rounds: 012 times, Percentage:000.1% Cumulative:97.96%
168 rounds: 009 times, Percentage:000.1% Cumulative:98.05%
169 rounds: 011 times, Percentage:000.1% Cumulative:98.16%
170 rounds: 014 times, Percentage:000.1% Cumulative:098.3%
171 rounds: 008 times, Percentage:000.1% Cumulative:98.38%
172 rounds: 009 times, Percentage:000.1% Cumulative:98.47%
173 rounds: 010 times, Percentage:000.1% Cumulative:98.57%
174 rounds: 011 times, Percentage:000.1% Cumulative:98.68%
175 rounds: 008 times, Percentage:000.1% Cumulative:98.76%
176 rounds: 005 times, Percentage:000.1% Cumulative:98.81%
177 rounds: 005 times, Percentage:000.1% Cumulative:98.86%
178 rounds: 004 times, Percentage:000.0% Cumulative:098.9%
179 rounds: 005 times, Percentage:000.1% Cumulative:98.95%
180 rounds: 004 times, Percentage:000.0% Cumulative:98.99%
181 rounds: 006 times, Percentage:000.1% Cumulative:99.05%
182 rounds: 004 times, Percentage:000.0% Cumulative:99.09%
...
248 rounds: 001 times, Percentage:000.0% Cumulative:99.97%
252 rounds: 001 times, Percentage:000.0% Cumulative:99.98%
254 rounds: 001 times, Percentage:000.0% Cumulative:99.99%
267 rounds: 001 times, Percentage:000.0% Cumulative:100.0%

181 rounds: 006 times, Percentage:000.1% Cumulative:99.05%

You can adjust the values, so instead of 100 choices let's say there were only 10 choices then it would be

Question 2: Part 1 Answer for 99% certainty for 10 choices is Round 14.

PGF and CDF of Rounds taken for 10 total choices and window size 5

Choosing 5 choices every round till all 10 choices are seen
3 rounds: 45 times, Percentage:4.5% Cumulative:4.5%
4 rounds: 167 times, Percentage:16.7% Cumulative:21.2%
5 rounds: 220 times, Percentage:22.0% Cumulative:43.2%
6 rounds: 210 times, Percentage:21.0% Cumulative:64.2%
7 rounds: 136 times, Percentage:13.6% Cumulative:77.8%
8 rounds: 80 times, Percentage:8.0% Cumulative:85.8%
9 rounds: 48 times, Percentage:4.8% Cumulative:90.6%
10 rounds: 39 times, Percentage:3.9% Cumulative:94.5%
11 rounds: 21 times, Percentage:2.1% Cumulative:96.6%
12 rounds: 10 times, Percentage:1.0% Cumulative:97.6%
13 rounds: 12 times, Percentage:1.2% Cumulative:98.8%
14 rounds: 4 times, Percentage:0.4% Cumulative:99.2%
15 rounds: 2 times, Percentage:0.2% Cumulative:99.4%
16 rounds: 3 times, Percentage:0.3% Cumulative:99.7%

Here is the Python code

import numpy as np
seen = []
history = []
total_choices = 100
window_size = 5
def choose():
  return list(np.random.choice(total_choices, window_size))
def keep_rolling():
  global seen
  global history
  new_seen = choose()
  seen = list(set([new_seen, seen]))
  history = [*history, new_seen]
def print_rounds():
tweak this while loop to total_choices*99/100 or any optimization number
while(len(seen) != total_choices):
    keep_rolling()
  #print(str(len(history)) + " rounds taken")
  #for x in history:
print(x)
return len(history)
trials = 10000
rounds = []
cumulative = 0
for i in range(trials):
  rounds_taken = print_rounds()
  rounds = [*rounds, rounds_taken]
  seen = []
  history = []
print(f"Choosing {window_size} choices every round till all {total_choices} choices are seen")
for x in list(sorted(list(set(rounds)))):
  count = len([y for y in rounds if y==x])
  percentage = count*100/trials
  cumulative = cumulative + percentage
  print(f"{str(x).zfill(3)} rounds: {str(count).zfill(3)} times, Percentage:{str(round(percentage, 1)).zfill(5)}% Cumulative:{str(round(cumulative, 2)).zfill(5)}%")

Each simulation takes around 5 seconds, and running it multiple times gives almost the same answers so the expected number of rounds is solved with no problem in variance.

At max instead of Round 181 it might be +- 4 rounds which is the Confidence Interval/Variance So to be on the safe side we can say Round 185 for 100 coupons, 5 draws per round.

If you calculate it theoretically, you'll get a smaller exact range such as 183 rounds +- 2 rounds for example to Question 1. Basically the distribution has a long tail that goes to infinity that we can cut and measure the area of by integration or binomial theorem for that last 1% probability.

Here are some solutions for Question 2 by changing the total choices from 100 to some other number

Choosing 5 choices every round till all 6 choices are seen
008 rounds: 063 times, Percentage:000.6% Cumulative:099.6%
Choosing 5 choices every round till all 7 choices are seen
009 rounds: 066 times, Percentage:000.7% Cumulative:99.26%
Choosing 5 choices every round till all 10 choices are seen
14 rounds: 4 times, Percentage:0.4% Cumulative:99.2%
Choosing 5 choices every round till all 20 choices are seen
030 rounds: 026 times, Percentage:000.3% Cumulative:99.05%
Choosing 5 choices every round till all 25 choices are seen
039 rounds: 017 times, Percentage:000.2% Cumulative:99.08%
Choosing 5 choices every round till all 30 choices are seen
047 rounds: 020 times, Percentage:000.2% Cumulative:99.08%
Choosing 5 choices every round till all 50 choices are seen
084 rounds: 010 times, Percentage:000.1% Cumulative:99.04%

If I run the simulation for 100 $\to$ 5 coupons 10 times it gives

Variance calculation/estimation

Choosing 5 choices every round till all 100 choices are seen
184 rounds: 010 times, Percentage:000.1% Cumulative:99.04%
Choosing 5 choices every round till all 100 choices are seen
181 rounds: 004 times, Percentage:000.0% Cumulative:099.0%
Choosing 5 choices every round till all 100 choices are seen
183 rounds: 006 times, Percentage:000.1% Cumulative:99.02%
Choosing 5 choices every round till all 100 choices are seen
184 rounds: 004 times, Percentage:000.0% Cumulative:99.02%
Choosing 5 choices every round till all 100 choices are seen
185 rounds: 004 times, Percentage:000.0% Cumulative:99.02%
Choosing 5 choices every round till all 100 choices are seen
185 rounds: 009 times, Percentage:000.1% Cumulative:99.04%
Choosing 5 choices every round till all 100 choices are seen
184 rounds: 006 times, Percentage:000.1% Cumulative:099.0%
Choosing 5 choices every round till all 100 choices are seen
184 rounds: 003 times, Percentage:000.0% Cumulative:99.02%
Choosing 5 choices every round till all 100 choices are seen
183 rounds: 004 times, Percentage:000.0% Cumulative:99.02%
Choosing 5 choices every round till all 100 choices are seen
184 rounds: 006 times, Percentage:000.1% Cumulative:99.04%

Question 1 Part 2 - Question 1 Completed

If the question starts at seen = "some coupons"? (k>n)

Lets say we have already seen 32 of the 100 total coupons and we are going to choose 5 tickets and we need to know how many rounds it will likely(99%) take? That is the same as running a calculation of total coupons = 100 - 32 = 68 total coupons with a window size of 5 and finding the row where the CDF crosses 99%. So if it took 51 rounds to see 32 coupons

Choosing 5 choices every round till all 68 choices are seen
119 rounds: 003 times, Percentage:000.0% Cumulative:99.01%

So it will take another 119 rounds to see the remaining 68 choices. So the total rounds it took was 51 + 119 = 170 total rounds to see all the 100 coupons. But if we say that it might take more as the 32 coupons can also be seen again - then it again goes back to the total coupons 100 and window size 5 calculation but with the starting point at 32 seen.

So we change the Python code starting lines as follows

already_seen = 32
print(f"Already seen {already_seen}")
seen = [x for x in range(already_seen)]
history = []
total_choices = 100
window_size = 5
...
replace seen = []
seen = [x for x in range(already_seen)]

And we get

Already seen 32
Choosing 5 choices every round till all 100 choices are seen
045 rounds: 001 times, Percentage:000.0% Cumulative:00.01%
046 rounds: 001 times, Percentage:000.0% Cumulative:00.02%
047 rounds: 003 times, Percentage:000.0% Cumulative:00.05%
048 rounds: 002 times, Percentage:000.0% Cumulative:00.07%
049 rounds: 003 times, Percentage:000.0% Cumulative:000.1%
...
126 rounds: 051 times, Percentage:000.5% Cumulative:89.05%
127 rounds: 041 times, Percentage:000.4% Cumulative:89.46%
128 rounds: 051 times, Percentage:000.5% Cumulative:89.97%
129 rounds: 047 times, Percentage:000.5% Cumulative:90.44%
130 rounds: 039 times, Percentage:000.4% Cumulative:90.83%
131 rounds: 043 times, Percentage:000.4% Cumulative:91.26%
132 rounds: 042 times, Percentage:000.4% Cumulative:91.68%
133 rounds: 034 times, Percentage:000.3% Cumulative:92.02%
134 rounds: 041 times, Percentage:000.4% Cumulative:92.43%
135 rounds: 037 times, Percentage:000.4% Cumulative:092.8%
136 rounds: 027 times, Percentage:000.3% Cumulative:93.07%
137 rounds: 033 times, Percentage:000.3% Cumulative:093.4%
138 rounds: 042 times, Percentage:000.4% Cumulative:93.82%
139 rounds: 030 times, Percentage:000.3% Cumulative:94.12%
140 rounds: 032 times, Percentage:000.3% Cumulative:94.44%
141 rounds: 028 times, Percentage:000.3% Cumulative:94.72%
142 rounds: 016 times, Percentage:000.2% Cumulative:94.88%
143 rounds: 025 times, Percentage:000.2% Cumulative:95.13%
144 rounds: 023 times, Percentage:000.2% Cumulative:95.36%
145 rounds: 022 times, Percentage:000.2% Cumulative:95.58%
146 rounds: 016 times, Percentage:000.2% Cumulative:95.74%
147 rounds: 010 times, Percentage:000.1% Cumulative:95.84%
148 rounds: 023 times, Percentage:000.2% Cumulative:96.07%
149 rounds: 015 times, Percentage:000.1% Cumulative:96.22%
150 rounds: 012 times, Percentage:000.1% Cumulative:96.34%
151 rounds: 008 times, Percentage:000.1% Cumulative:96.42%
152 rounds: 018 times, Percentage:000.2% Cumulative:096.6%
153 rounds: 021 times, Percentage:000.2% Cumulative:96.81%
154 rounds: 017 times, Percentage:000.2% Cumulative:96.98%
155 rounds: 012 times, Percentage:000.1% Cumulative:097.1%
156 rounds: 019 times, Percentage:000.2% Cumulative:97.29%
157 rounds: 013 times, Percentage:000.1% Cumulative:97.42%
158 rounds: 014 times, Percentage:000.1% Cumulative:97.56%
159 rounds: 010 times, Percentage:000.1% Cumulative:97.66%
160 rounds: 008 times, Percentage:000.1% Cumulative:97.74%
161 rounds: 009 times, Percentage:000.1% Cumulative:97.83%
162 rounds: 011 times, Percentage:000.1% Cumulative:97.94%
163 rounds: 007 times, Percentage:000.1% Cumulative:98.01%
164 rounds: 006 times, Percentage:000.1% Cumulative:98.07%
165 rounds: 011 times, Percentage:000.1% Cumulative:98.18%
166 rounds: 007 times, Percentage:000.1% Cumulative:98.25%
167 rounds: 018 times, Percentage:000.2% Cumulative:98.43%
168 rounds: 005 times, Percentage:000.1% Cumulative:98.48%
169 rounds: 009 times, Percentage:000.1% Cumulative:98.57%
170 rounds: 013 times, Percentage:000.1% Cumulative:098.7%
171 rounds: 006 times, Percentage:000.1% Cumulative:98.76%
172 rounds: 003 times, Percentage:000.0% Cumulative:98.79%
173 rounds: 013 times, Percentage:000.1% Cumulative:98.92%
174 rounds: 003 times, Percentage:000.0% Cumulative:98.95%
175 rounds: 005 times, Percentage:000.1% Cumulative:099.0%
177 rounds: 004 times, Percentage:000.0% Cumulative:99.04%
178 rounds: 002 times, Percentage:000.0% Cumulative:99.06%
179 rounds: 002 times, Percentage:000.0% Cumulative:99.08%
180 rounds: 006 times, Percentage:000.1% Cumulative:99.14%
181 rounds: 004 times, Percentage:000.0% Cumulative:99.18%
182 rounds: 004 times, Percentage:000.0% Cumulative:99.22%
183 rounds: 004 times, Percentage:000.0% Cumulative:99.26%
184 rounds: 005 times, Percentage:000.1% Cumulative:99.31%
185 rounds: 003 times, Percentage:000.0% Cumulative:99.34%
186 rounds: 003 times, Percentage:000.0% Cumulative:99.37%
187 rounds: 002 times, Percentage:000.0% Cumulative:99.39%
188 rounds: 002 times, Percentage:000.0% Cumulative:99.41%
189 rounds: 003 times, Percentage:000.0% Cumulative:99.44%
190 rounds: 001 times, Percentage:000.0% Cumulative:99.45%
191 rounds: 003 times, Percentage:000.0% Cumulative:99.48%
192 rounds: 004 times, Percentage:000.0% Cumulative:99.52%
194 rounds: 001 times, Percentage:000.0% Cumulative:99.53%
195 rounds: 001 times, Percentage:000.0% Cumulative:99.54%
196 rounds: 002 times, Percentage:000.0% Cumulative:99.56%
197 rounds: 004 times, Percentage:000.0% Cumulative:099.6%
198 rounds: 004 times, Percentage:000.0% Cumulative:99.64%
199 rounds: 005 times, Percentage:000.1% Cumulative:99.69%
200 rounds: 002 times, Percentage:000.0% Cumulative:99.71%
201 rounds: 001 times, Percentage:000.0% Cumulative:99.72%
203 rounds: 001 times, Percentage:000.0% Cumulative:99.73%
205 rounds: 001 times, Percentage:000.0% Cumulative:99.74%
207 rounds: 004 times, Percentage:000.0% Cumulative:99.78%
208 rounds: 003 times, Percentage:000.0% Cumulative:99.81%
209 rounds: 001 times, Percentage:000.0% Cumulative:99.82%
210 rounds: 001 times, Percentage:000.0% Cumulative:99.83%
212 rounds: 002 times, Percentage:000.0% Cumulative:99.85%
213 rounds: 002 times, Percentage:000.0% Cumulative:99.87%
214 rounds: 001 times, Percentage:000.0% Cumulative:99.88%
217 rounds: 001 times, Percentage:000.0% Cumulative:99.89%
219 rounds: 001 times, Percentage:000.0% Cumulative:099.9%
220 rounds: 001 times, Percentage:000.0% Cumulative:99.91%
221 rounds: 001 times, Percentage:000.0% Cumulative:99.92%
225 rounds: 001 times, Percentage:000.0% Cumulative:99.93%
226 rounds: 001 times, Percentage:000.0% Cumulative:99.94%
229 rounds: 001 times, Percentage:000.0% Cumulative:99.95%
235 rounds: 001 times, Percentage:000.0% Cumulative:99.96%
237 rounds: 001 times, Percentage:000.0% Cumulative:99.97%
244 rounds: 001 times, Percentage:000.0% Cumulative:99.98%
252 rounds: 001 times, Percentage:000.0% Cumulative:99.99%
279 rounds: 001 times, Percentage:000.0% Cumulative:100.0%

175 rounds: 005 times, Percentage:000.1% Cumulative:099.0%

So it took an extra 175 rounds in addition to the rounds it took to see the 32 coupons initially.

Question 2 Part 2 Completed

If it is not known that there are 100 coupons

Somehow you would have to give information on how many rounds we are allowed to use to estimate the total unknown number of coupons and the uncertainty in our estimate of this unknown total number. If there is no limit we can simply run many trials until we stop seeing new numbers - the stopping condition will be influenced by 3 things -

1. how many total trials we ran.
2. how many trials since we last saw a new number.
3. how many new numbers have we seen in total. This would also require some numerical calculation.

Already seen 32
100 rounds, unknown 303 choices, observed coupons seen
100 rounds, 0032.0 coupons seen, Actual coupon count: 032
100 rounds, 0033.0 coupons seen, Actual coupon count: 033
100 rounds, 0034.0 coupons seen, Actual coupon count: 034
100 rounds, 0035.0 coupons seen, Actual coupon count: 035
100 rounds, 0036.0 coupons seen, Actual coupon count: 036
100 rounds, 0037.0 coupons seen, Actual coupon count: 037
100 rounds, 0038.0 coupons seen, Actual coupon count: 038
100 rounds, 0039.0 coupons seen, Actual coupon count: 039
100 rounds, 0040.0 coupons seen, Actual coupon count: 040
100 rounds, 0041.0 coupons seen, Actual coupon count: 041
100 rounds, 0042.0 coupons seen, Actual coupon count: 042
100 rounds, 0043.0 coupons seen, Actual coupon count: 043
...
100 rounds, 095.67 coupons seen, Actual coupon count: 096
100 rounds, 096.57 coupons seen, Actual coupon count: 097
100 rounds, 097.61 coupons seen, Actual coupon count: 098
100 rounds, 098.65 coupons seen, Actual coupon count: 099
100 rounds, 099.38 coupons seen, Actual coupon count: 100
100 rounds, 100.68 coupons seen, Actual coupon count: 101
100 rounds, 101.33 coupons seen, Actual coupon count: 102
100 rounds, 102.16 coupons seen, Actual coupon count: 103
100 rounds, 103.38 coupons seen, Actual coupon count: 104
...
100 rounds, 241.13 coupons seen, Actual coupon count: 287
100 rounds, 242.92 coupons seen, Actual coupon count: 288
100 rounds, 242.84 coupons seen, Actual coupon count: 289
100 rounds, 244.23 coupons seen, Actual coupon count: 290
100 rounds, 245.96 coupons seen, Actual coupon count: 291
100 rounds, 244.69 coupons seen, Actual coupon count: 292
100 rounds, 245.07 coupons seen, Actual coupon count: 293
100 rounds, 246.15 coupons seen, Actual coupon count: 294
100 rounds, 247.56 coupons seen, Actual coupon count: 295
100 rounds, 247.08 coupons seen, Actual coupon count: 296
100 rounds, 0247.0 coupons seen, Actual coupon count: 297
100 rounds, 249.77 coupons seen, Actual coupon count: 298
100 rounds, 249.12 coupons seen, Actual coupon count: 299
100 rounds, 248.28 coupons seen, Actual coupon count: 300
100 rounds, 250.57 coupons seen, Actual coupon count: 301
100 rounds, 250.46 coupons seen, Actual coupon count: 302
100 rounds, 252.53 coupons seen, Actual coupon count: 303
100 rounds, 250.06 coupons seen, Actual coupon count: 304
100 rounds, 253.05 coupons seen, Actual coupon count: 305
...
100 rounds, 0318.7 coupons seen, Actual coupon count: 475
100 rounds, 321.94 coupons seen, Actual coupon count: 476
100 rounds, 321.56 coupons seen, Actual coupon count: 477
100 rounds, 321.42 coupons seen, Actual coupon count: 478
100 rounds, 321.94 coupons seen, Actual coupon count: 479
100 rounds, 322.56 coupons seen, Actual coupon count: 480
100 rounds, 321.94 coupons seen, Actual coupon count: 481
100 rounds, 320.27 coupons seen, Actual coupon count: 482
...
100 rounds, 325.26 coupons seen, Actual coupon count: 495
100 rounds, 325.77 coupons seen, Actual coupon count: 496
100 rounds, 327.29 coupons seen, Actual coupon count: 497
100 rounds, 325.05 coupons seen, Actual coupon count: 498
100 rounds, 0328.0 coupons seen, Actual coupon count: 499
Coupons seen -> Probability through Maximum Likelihood Estimation of prior probabilities

Would need MLE to calculate the PDF and CDF for coupons seen $\to$ total coupons estimated.

Around 328 coupons seen in 100 rounds points to the total coupon count being around 500.

Around 100 coupons seen in 100 rounds points to the total coupon count being around 100.

Maximum possible seen coupons in 100 rounds = 500.

If we observed 500 new coupons for 100 rounds at 5 coupons per round then the expected total coupons is $\infty$

If 450 coupons are seen it means the estimated total coupons are around 1500.

If 400 coupons are seen it means the estimated total coupons are around 900.

It seems the expected total coupons keep doubling the closer we half the distance to reach to 500 maximum for 5 selected every round for 100 rounds.

Python code for APriory generation shown above.

import numpy as np
already_seen = 32
print(f"Already seen {already_seen}")
seen = [x for x in range(already_seen)]
window_size = 5
def choose(total_choices):
  return list(np.random.choice(total_choices, window_size))
def keep_rolling(total_choices):
  global seen
  new_seen = choose(total_choices)
  seen = list(set([seen, new_seen]))
def get_seen():
  total_choices = already_seen + np.random.randint(468)
unknown total coupons, between 32 and 500
for x in range(100):
    keep_rolling(total_choices)
  return [len(seen), total_choices]
trials = 10000
seen_frequency = {}
cumulative = 0
for i in range(trials):
  [seen_count, total_choices] = get_seen()
  if total_choices in seen_frequency.keys():
    seen_frequency[total_choices] = [*seen_frequency[total_choices], seen_count]
  else:
    seen_frequency[total_choices] = [seen_count]
  seen = [x for x in range(already_seen)]
print(f"100 rounds, unknown {total_choices} choices, observed coupons seen")
for x in list(sorted(seen_frequency.keys())):
  count = round(sum(seen_frequency[x]) / len(seen_frequency[x]), 2)
  print(f"100 rounds, {str(count).zfill(6)} coupons seen, Actual coupon count: {str(x).zfill(3)}")
print("Coupons seen -> Probability through Maximum Likelihood Estimation of prior probabilities")

Points of Clarity from Questions asked

Is it good enough to have a Python program to plug in the values 5 and 100 to any values of your choosing?

It would be much simpler to start with 5 of 6, and 5 of 20, than 5 of 100. Is there any significance to

• 99% certainty
• 100 total choices
• Window size of 5
• the variable "n" was used twice, it needs to be unique in question. probably need to fix the definition of "n", "m", "k", "j", "x" and the other variables properly
• your question implies that you want to know when you've seen 99% of the choices, any reason why we would stop at having seen 99% of the total choices? The second question implies calculation for having seen 99% of the total choices 1-100 or 99th percentile in CDF?
• assuming you meant 99% of the total coupons seen, what confidence interval do you want for the 99% PDF? If not specified, it will default to 95% confidence interval over the 99% total coupons seen.

Answer 3

Theoretical Analysis of the Problem on Stochastic Processes

There is a distinction between Coupon collector's problem and X balls in Y turns. As far as I can see, nowhere in Coupon collector's does it state that 5 coupons can be selected together out of 100 coupons with replacement. The Coupons are selected one at a time, with replacement. Selecting 5 of them would require not replacing the coupons until all 5 are drawn together. There is a difference between $\frac{1}{100}^{5}$ and $\frac{1}{100}\frac{1}{99}\frac{1}{98}\frac{1}{97}\frac{1}{96}$ so the two problems are not alike at all - Coupon Collector vs X balls in y turns

$5\binom{100}{1} = \frac{100!}{(99!)1!}$ is nothing equal to

$\binom{100}{5} = \frac{100!}{(95!)5!}$

1. Stochastic processes involve a random variable X, which has PGF, PDF, PMF and CDF to calculate Expectation E(X) and Confidence Intervals using Variance Var(X). Expectation is called the first moment of the PGF and the Variance is the second 'central' moment of the PGF. The third 'normalized' moment calculates skewness and the fourth 'normalized' moment defines kurtosis.
   The PGF or Probability Generating Function is used to generate probability. However for stochastic processes of discrete variable X (such as selecting coupons based on round number) we have to use PMF or Probability Mass Function pmf(X). The Moment Generating Function MGF is used to calculate the first and second moments for E(X) and Var(X).

Discrete Probability Distribution

Probability Mass Function PMF

2. It is important to understand the Central Limit Theorem (CLT) for a normal variable X to have basic idea about Expectation, Standard Deviation and Variance. For example: A fair coin has 50% chance for Heads and 50% chance for tails. So In 1 coin toss, Expectation(Heads) = E(H) = 0.5 = 50%. If I want Expectation(H) = 1 = 100% then 2 coin toss gives E(H) = 1 = 100%. What this means is I expect to see a heads after 2 coin tosses. But if you calculate the probability, in 2 coin tosses 0.5 + 0.25 = 0.75, so only a 75% chance of heads at least once. This emphasizes the distinction between definition of Expectation and Probability. This has to do with normal distribution being generated out of binomial distribution being generated out of bernoulli distribution. A coin toss has a bernoulli variable of 50% Heads and 50% tails so it is basically choosing {H, T} uniformly which can be represented as {0, 1} or {1, 2} . A discrete variable X like coupons or balls will always be related to normal distribution through the CLT. The CLT defines the normal distribution expectation as $68.27$% probability around 2 standard deviations $\sigma$ around E. So

$E \pm \sigma$ = 68.27% of the total probability - CI $2\sigma$ and

$E \pm 2\sigma$ = 95.45% of the total probability - CI $4\sigma$ and

$E \pm 3\sigma$ = 99.73% of the total probability - Confidence interval $6\sigma$

We calculate the Variance using the Law of Large Numbers.

For solving Coupon Collector's problem in the simplest way, we will need the Martingale variant of CLT for Expectation and Variance calculation.

Normal Distribution

Central Limit Theorem

Martingale Difference CLT

Martingale CLT

3. For eliminating errors in Expectation calculation of Round number two things must be done

• Variance calculations Var(X) and Standard Deviation $\sigma$
• Remove two tails from the distribution using variance and $\sigma$ - one at 0% and the other at 100%.

Methods for calculating Variance

• Chebyshev inequality
• Markov inequality, which is better and more precise

Markov's inequality for variance calculation

To solve the Coupon Collector's problem - we can use Martingale

Martingale solution of Coupon Collector's problem

Coupon Collector solutions

• via generating functions using Stirling number's of the second kind, it became an algebraic period to generate probability.
• calculating the expectation requires geometric distribution. By adding 5 variables $5\binom{100}{1}$ will become t1 + t2 + t3 + t4 + t5. Using the Euler Mascheroni constant the Harmonic number will give the Expectation for n. It even has a variation for n-k when k numbers are already seen.
• martingales

Martingale is a special Markov chain where the previous state does not matter. So having drawn i coupons and seen i coupons, will not affect the next j coupons to be seen. Therefore Martingale M(j|i) = M(j) and we can ignore the i coupons seen already. In every transition the state changes as follows

probability of next round seeing new coupon = $\frac{5}{100}$

probability of next round not seeing new coupon = $1 - \frac{5}{100} = \frac{95}{100}$

Take variable t to mean the not yet seen coupons $t \to 0$ as the rounds progress.

Let's say we are seeing 1 coupon out of total 1 coupon, then Expectation = 1

For seeing both of 2 coupon, one coupon at a time,

Round 1 -> We see 1 coupon

Expectation(Round 1) = 0.5 = 50% seen

Round 2 -> We have 50% chance to see second coupon

Expectation(Round 2) = 0.5 + 0.25 = 75% seen

...

Round 7

Expectation(Round 7) = 0.5 + 0.25 + 0.125 + 0.0625 + 0.0625/2 + 0.0625/4 + 0.0625/8 = 99.22% seen

At round 7 we have seen 99% of the coupons.

Now the calculation of $e^{-e^{-1}} = 0.6922 = 69.22$% and $e^{-e^{-2}} = 0.8734 = 87.34$%

and $e^{-e^{-3}} = 0.9514 = 95.14$%

The formula states $e^{-e^{-c}} = Pr(0)$ for c=0, 1, 2, 3 ... gives the Pr(0) for desired c limit.

For the kth probability we get a simple Poisson Distribution

Pr(N = k) = $\frac{e^{-kc}}{k!} Pr(0) = \frac{e^{-kc}}{k!}e^{-e^{-c}}$

How the coefficient affects Pr(0)

Using this we can calculate all the moments required such as Expectation and Variance for selecting 1 coupon per round for 2 coupons total.

Now I am not exactly sure how to generalize this to 5 select out of 100 coupons but it should be straightforward from here.

Plus the 99% seen will itself pose an additional challenge in discrete random variable X but for most part it is simply 0.99*100 coupons = Expectation(99 coupons) .

• Especially if the 5 are selected together it will not look anything like the Coupon Collector's problem.

• It does not seem like X balls in Y turns has similarity to hyper-geometric distribution. It seems it is simple nCr of binomial theorem and multinomial theorem and falls under binomial distribution and multinomial distribution for $\binom{100}{5}$.

Binomial Distribution

Expectation and Variance in Binomial Distribution for X coins in Y turns

Binomial Distribution - Expectation and Variance formula

For 5 balls selected every turn out of 100, it can be calculated with a matrix multiplication for Expectation and Variance in Multinomial distribution.

Multinomial Distribution - Expectation and Variance matrix formula