8

Background

There are a number of functions that are subject to "Sum = Integral" identities. Some of them are listed in this question. For instance, when we set $ {\rm sinc}\, x := \sin(x)/x \,$, we have

$$\int_{-\infty}^{+\infty} {\rm sinc}\, x \, dx = \sum_{n = -\infty}^{+\infty} {\rm sinc}\, n = \pi. \tag{1}\label{1}$$ More generally, the equality: $$\int_{-\infty}^{+\infty} {\rm sinc}^k\, x \, dx = \sum_{n = -\infty}^{+\infty} {\rm sinc}^k\, n \tag{2}\label{2}$$ holds for $k = 1,2,\ldots, 6$.

Moreover, user Argon mentions in his answer a similar identity that holds for the Bessel function of the first kind:

$$\int_{-\infty}^\infty \frac{J_y (at) J_y(bt)}{t}\, \text{d}t=\sum_{t=-\infty}^\infty \frac{J_y (at) J_y(bt)}{t}. \tag{3}\label{3}$$

Functional square root of the sine

I wonder whether a similar identity holds for the power series one obtains for the function $f(\cdot)$ that satisfies $f(f(x)) = \sin(x)$. More information about this series can be found over here. We have:

\begin{align} f ={} & x - \frac{x^3 }{ 12} - \frac{x^5 }{ 160} - \frac{53 x^7 }{ 40320} - \frac{23 x^9 }{71680} - \frac{92713 x^{11}}{1277337600} \\[10pt] & - \frac{742031 x^{13} }{79705866240} + \frac{594673187 x^{15} }{167382319104000} + \frac{329366540401 x^{17} }{91055981592576000} \\[10pt] & +\frac{104491760828591 x^{19} }{62282291409321984000} + \frac{1508486324285153 x^{21} }{4024394214140805120000} \pm \cdots \end{align}

The numerators and denominators are listed in this and this OEIS entry, respectively.

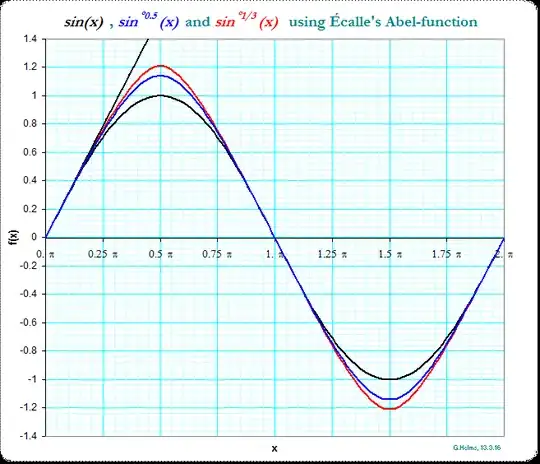
The functional square root of the sine can also be represented by means of a Laurent series, as explained by user Will Jagy in an answer to his own question. Gottfried Helms plots the fractional iterates of the sine with this Laurent series expansion as follows:

enter image description here

We see that the functional square root (the half iterate, in blue) is slightly more pointy than the original sine function (in black). Apart from that, it does not appear to be too different from the sine.

A similar picture emerges when one computes the functional square root of the sine with its corresponding Newton series, as explained by user Anixx.

Question

Set $h(x) := f(x)/x$ to dampen the original half-iterate. Does a "Sum = Integral" identity hold for $h(\cdot)$, similar to the identities \eqref{1} through \eqref{3} ?

Max Lonysa Muller
  • 7,546
  • 1
    Most functions don't satisfy this identity, of course. Do you have any specific reason to suspect that $h(x)$ does? Have you even shown that the integral and sum are well-defined? (They certainly don't seem absolutely convergent, for example.) – Greg Martin Jul 26 '24 at 17:15
  • 1
    @GregMartin I suspect this is true because $f(\cdot)$ shares a number of important properties with the sine. First, it is also an odd function. Second, $f(x) = 0$ at $x = k \cdot \pi$ for $k \in \mathbb{Z} $. Finally, it is both bounded and periodic. I would've liked to support my intuition with numerical evidence, but it seems to be hard to approximate $h(\cdot)$ precisely enough with its power series so as to be able to reliably calculate the sum and integral. I have not yet shown that these quantities are well-defined – Max Lonysa Muller Jul 26 '24 at 19:38
  • 1
    $\sin(\sin x)$ has all the properties you mention as well, and is even more closely related to $f(x)$. Can you determine whether the sum equals the integral for $\sin(\sin x)/x$? Numerical calculations look unpromising, though the error terms are too large for me to tell. – Greg Martin Jul 27 '24 at 01:14
  • I’d +100 this post and comments, for their interest and novelty, if I could. – A rural reader Jul 27 '24 at 03:43
  • I think, it holds for any periodic function with irrational period... – Anixx Apr 16 '25 at 08:17
  • @Anixx why do you think irrationality of the period is required? – Max Lonysa Muller Apr 16 '25 at 10:25
  • Just speculation – Anixx Apr 16 '25 at 10:30

0 Answers0