The problem $F_n(n)\geq\frac12$ is equivalent to mean $\mu$ $\geq$ median $m$ for any $\chi^2$ distribution. In the following, I will not impose the $n\in\mathbb{N}$ condition, but allow $n\geq0$. And I will establish strict inequality $F_n(n)>\frac12$.
- The degenerate case with $n=0$.
Trivially, $F_0(0)=1 > \frac12$ and $\mu=m=0$. As we will see, this is the only situation where $\mu=m$, but the inequality $F_0(0)>\frac12$ is still strict.
- The case of $0<n\leq2$ with a strictly decreasing pdf $f_n(x)$.
Reflect the left side of the pdf $f_n(x)$ about median $m$ to the right side and call the resulting curve $h(x)$, i.e.,
$$h(x)=
\begin{cases} f_n(x), &\text{ if }0\leq x \leq m,\\
f_n(2m-x), &\text{ if }m<x<2m,\\
0, &\text{ otherwise}.
\end{cases}
$$
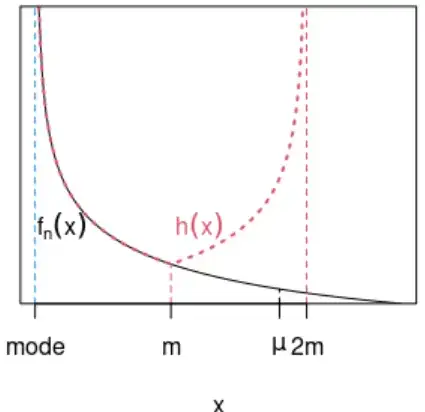
Obviously, $h(x)$ is a pdf since the area under $h$ is twice the area ($0.5$) to the left of $m$. Let $H(X)$ be the corresponding cdf and $\mu_H$ be the mean, which is just $m$ due to symmetry of $h(x)$ by construction.
- For the left side $x\leq m$, the two curves match and $H(x)=F_n(x)$.
- For the middle region $m< x<2m$, because $f_n(x)$ is strictly decreasing, the reflected portion $h(x)=f_n(2m-x)$ is increasing and must be $>f_n(x)$ . Thus the areas under the curves must be $H(x) > F_n(x)$ for all $m< x < 2m$.
- For the right side $x\geq2m$, trivially $H(x)=1>F_n(x)$.
In summary, $H(x)\geq F_n(x)$ all $x$ with strict inequality for $x>m$, and we established a stochastic order between $H$ and $F_n$. It follows that,
$$
\mu=\int_0^\infty 1-F_n(x)\,\mathbb{d}x > \int_0^\infty 1-H(x)\,\mathbb{d}x
=\mu_H=m.
$$
- The case with $n>2$.

In this case, $h(x)$ is defined exactly as above. However, as the mode $n-2>0$, the reflected portion $h(x)=f(2m-x)$ is not necessarily larger than $f_n(x)$ for $m<x<2m$. Define their log density ratio as
$$
r(t) = \log\left[\frac{h(m+t)}{f_n(m+t)}\right] = \log\left[ \frac{f_n(m-t)}{f_n(m+t)}\right],\ 0\leq t<m
$$
which can be simplified to
$$
r(t)=t+\frac{n-2}2 \log\left[\frac{m-t}{m+t}\right].
$$
Its second derivative is
$$
r''(t)=-\frac{2(n-2)mt}{\left(m^2-t^2\right)^2}<0
$$
for $0<t<m$. Thus, $r(t)$ is strictly concave over $(0,m)$. But
$$ \begin{align}
r(0)&=0,\\
\lim_{t\rightarrow 0^+} r'(t)&=1-\frac{n-2}m >0,\text{ and} \tag{">" to be verified later}\\
\lim_{t\rightarrow m^-} r(t)&=-\infty.
\end{align}$$
Therefore, the strictly concave $r(t)$ is initially increasing from $0$ and eventually decreasing to $-\infty$. There will be exactly one point $t_0\in(0,m)$ such that $r(t_0)=0$, corresponding to $x_0=m+t_0\in(m,2m)$ at which $h(x)$ crosses $f_n(x)$ from above. That is,
- For the left side $x\leq m$, the two curves match and $F_n(x)=H(x)$.
- For the middle region $m< x \leq x_0$, we have $h(x)\geq f_n(x)$ and thus their cdf's satisfy $F_n(x)\leq H(x)$.
- For the right side $x> x_0$, we have $h(x) < f_n(x)$ strictly and thus
$$\begin{align}
F_n(x) &= 1-\int_{x}^\infty f_n(x)\,\mathbb{d}x \\
&< 1-\int_{x}^\infty h(x)\,\mathbb{d}x\\
&=H(x).
\end{align}$$.
In summary, $F_n(x)\leq H(x)$ for all $x$ with strict inequality at least for $x>x_0$, and we, again, established a stochastic order between $H$
and $F_n$. So, as in the previous case,
$$
\mu=\int_0^\infty 1-F_n(x)\,\mathbb{d}x > \int_0^\infty 1-H(x)\,\mathbb{d}x
=\mu_H=m.
$$
This confirms that $\mu>m$ for $n>2$, except for the $\lim_{t\rightarrow 0^+}r'(t)>0$ condition above to be verified.
To show $\lim_{t\rightarrow 0^+}r'(t)=1-\frac{n-2}m >0$, note that $n-2$ is the mode of $\chi^2_n$ distribution if $n>2$, and we only need to establish the "mode<median" inequality. (Actually, the "mode<media<mean" inequalities are usually stated together for "nice" distributions like the $\chi^2$ here.)
The proof follows the same idea of reflecting the pdf $f_n(x)$, but this time about the mode $n-2$. Define the reflected function $g$ by
$$
g(x)=\begin{cases}f_n(x),&\text{ if}\ 0<x\leq n-2,\\
f_n\left[2(n-2)-x\right],&\text{ if}\ n-2<x<2(n-2),\\
0,&\text{ otherwise}.
\end{cases}
$$
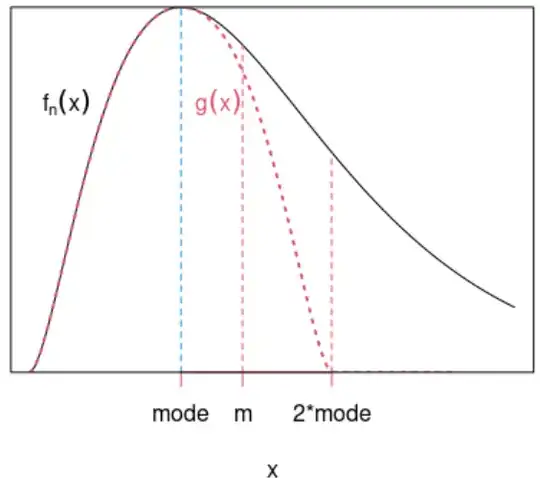
Note that, as we well see later, unlike $h$, the function $g$ is not a density, since its integral is $<1$. First, we establish $g(x)<f_n(x)$ for $n-2<x<2(n-2)$ by similar arguments. For $0\leq t<n-2$, define the log ratio
$$
q(t)=\log\left\lbrace \frac{g[(n-2)+t]}{f_n[(n-2)+t]} \right\rbrace
=\log\left\lbrace \frac{f_n[(n-2)-t]}{f_n[(n-2)+t]} \right\rbrace
$$
that simplifies to
$$
q(t)=t+\frac{n-2}{2} \log\left[ \frac{(n-2)-t}{(n-2)+t} \right],
$$
with its first derivative
$$q'(t) =\frac{t^2}{t^2-(n-2)^2} < 0\text{ for }0<t<n-2.
$$
Thus, starting from $q(0)=0$, the log ratio $q(t)$ decreases and $q(t)<0$ for all $0<t<n-2$. Namely, $g(x)<f_n(x)$ for $n-2<x<2(n-2)$.
Therefore, $g(x)\leq f_n(x)$ for all $x$ with strict inequality for $x>n-2$. Consequently, the total area under $g$ is strictly less than the total area $1$ under $f_n(x)$, and half of the area under $g$ is $<1/2$. But, by symmetry of $g$,
$$
\frac12\int_0^{2(n-2)}g(x)\,\mathbb{d}x=\int_{0}^{n-2}g(x)\,\mathbb{d}x = \int_{0}^{n-2}f_n(x)\,\mathbb{d}x <\frac12,
$$where the last inequality means that the median $m$ is to the right of the mode $n-2$. This ensures that
$$\lim_{t\rightarrow 0^+}r'(t)=1-\frac{n-2}m >0.
$$
To sum up, $F_n(n)>\frac12$ for all $n\geq0$ in the a $\chi^2_n$ distribution. Although the details may vary, the general idea of this proof is all about reflecting the pdf at some point of interest.


