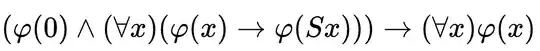-1

I am new to this topic, so sorry if some questions are stupid.

I have several questions to the Peano axioms:

  1. Why are the axioms 5 and 7 defined like that? How exactly they contribute to definition of $+$ and $*$? Can't these operations be defined another way? It just doesn't seem as intuitive as the rest of the axioms, which look super clear.

  2. I want to see any interesting situations that would occur if one (or more) of these axims wasn't there. I saw somewhere an image of a domino in a circle, with a comment that without some axioms, the rest could give a structure like that and still follow them. Can't remember what it was, maybe the induction axiom?

  3. I also want to see source of deriving commutativity, associtivity and other properties of the operations from the axioms.

Any insights are appreciated.

The images are from Wikipedia.

enter image description here

enter image description here

amWhy
  • 210,739
Tereza Tizkova
  • 2,750
  • 1
    $Sx \neq 0$ is the axiom that prevents circular structures. Otherwise you could loop around to $0$ at some point. The definition of addition and multiplication are the usual ones you learn in grade school. – CyclotomicField Jul 22 '24 at 16:18
  • 7
    Please do not use images to convey critical mathematical information not otherwise present in your post. Everything you write as an image can be typed. Here are some of the reasons you should not use images. – Arturo Magidin Jul 22 '24 at 16:22
  • 4
    Please ask one question per post. Each of your individual questions is quite substantial and would require a substantial answer. – Lee Mosher Jul 22 '24 at 16:47
  • Maybe relevant: https://math.stackexchange.com/questions/149944/peano-postulates – MJD Jul 22 '24 at 17:36
  • 5 and 7 are completely natural and intuitive one you realize you have to define addition/multiplication recursively. If you've defined $a+b$ up to a certain $a,b$ and you must define $a + $ the successor of $b$, definining it as $\text{the successor of }(a+b)$ is elagent and succinct. – fleablood Jul 23 '24 at 05:29
  • "I saw somewhere an image of a domino in a circle, with a comment that without some axioms, the rest could give a structure like that and still follow them. " Avoiding axiom one that $0$ is not a successor could do it. Say $0,1,2,3,4$ are as usual but $s(4) =0$ then you get $0<1<2<3<4<0<1....$. Forgetting induction we could have a number $\omega$ where you can never count to omega and it is "larger" than all natural numbers. Also without induction you could have numbers between $0$ and $1$ and between $n$ and $n+1$. – fleablood Jul 23 '24 at 05:36
  • See here for commutativity of sum and here for product. – Mauro ALLEGRANZA Jul 23 '24 at 14:02
  • See associativity – Mauro ALLEGRANZA Jul 23 '24 at 14:06

2 Answers2

1

The entire point of the Peano axioms is to define a structure that behaves the way we already expect the natural numbers to behave. In other words, it is an axiomatisation of the way we intuitively understand arithmetic.

For the recursive definitions of addition and multiplication in particular, those are there because we want to have a finite number of axioms but need to define operations that will work on an infinite number of elements.

Think about how you would create a set of axioms that lets you add 2+2 but also 100+5924 - and if you think in terms of how we learn to do addition in the first place, then it's all about counting, and in some sense you can imagine that you start with the number on the left and count up from it as many times as the number on the right, i.e.

$$\begin{eqnarray}(2) + (2) & = & (2) + (1 + 1) \\ & = & (2 + 1) + (1) \\ & = & ((2 + 1) + 1)\end{eqnarray}$$

and if we replace those $+1$ terms with applications of the successor function that leads us to something that looks a bit like axiom 5.

ConMan
  • 27,579
0

A more modern and concise of version of Peano's Axioms can be found here.

Removing the induction axiom, for example, would allow for a structure in which some elements may be isolated from the rest, i.e. it would not be possible to reach those elements by repeated application of the successor function starting from zero. A number might be its own successor!

Dan Christensen
  • 15,710