What is the toughness of the Tutte graph?

Question

The Tutte graph

is a $3$-regular graph with $46$ vertices and $69$ edges named after W. T. Tutte.

The toughness $\tau$ of a graph $G$ is

$$\tau(G)=\min_{S} \left\{\frac{|S|}{c(G-S)}\right\},$$

where $c(G)$ denotes the number of connected components of a graph $G$, and the minimum is taken over all $S$ that are cutsets of vertices in $G$.

We know that Tutte graph is non-Hamiltonian. I'm curious about what its toughness is equal to. A weak question is, is its toughness greater than or equal to $1$?

My motivation is to know whether the non-Hamiltonian property of Tutte graph can be explained by its toughness.

Answer 1

One way to answer the weak question is the following. Suppose a graph $G$ has two adjacent vertices $u$ and $v$ such that $G-u$ and $G-v$ are Hamiltonian. Then $G$ is $1$-tough. To prove this, suppose we remove $k$ vertices and there are more than $k$ components. Since $G-u$ is $1$-tough, at most $k$ of these components can intersect $G-u$, i.e. one component must be $\{u\}$. But the same applies to $v$, which is a contradiction since they are adjacent.

Now removing either of the marked vertices allows a path through the bottom fragment, from bottom left to bottom right, covering the remaining vertices, and such a path can be extended to a Hamilton cycle.

Answer 2

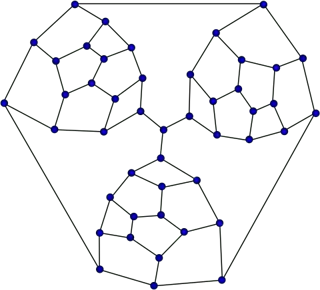
A computer search confirms that the toughness is $\frac87$. Here is a way we can achieve this, creating $7$ components by deleting $8$ vertices:

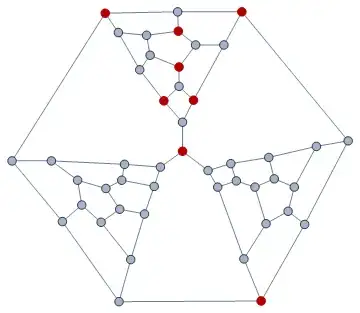
The Tutte graph has too many vertices to analyze by brute force, so here is the alternate strategy we will use.

Consider the Tutte fragment: the graph below. (The Tutte graph is obtained by stitching three of these together.)

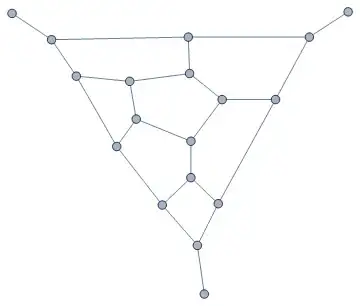
We will consider candidate vertex sets $S$ to delete from the interior of the Tutte fragment (that is, excluding the three degree-$1$ vertices) under several hypotheses:

• Each of the three degree-$1$ vertices may be present or already deleted.
• For the degree-$1$ vertices that are present, they may be connected to each other outside the fragment or not.

Here is a list of the $15$ possible hypotheses, in a shorthand notation: $\{\}$, $\{1\}$, $\{2\}$, $\{3\}$, $\{1,2\}$, $\{12\}$, $\{1,3\}$, $\{13\}$, $\{2,3\}$, $\{23\}$, $\{1,2,3\}$, $\{12,3\}$, $\{1,23\}$, $\{13,2\}$, $\{123\}$. (I write $1$, $2$, and $3$ to indicate which vertices are present, and write them together as $12$ if they are connected and separately as $1,2$ if not.)

Under each hypothesis, we will find the optimal $S$ to delete (the one that leaves the most connected components) for each value of $|S|$. We should feel free to exclude sets that don't do better than a smaller set (for instance, a $7$-vertex set that leaves $4$ components is always worse than a $5$-vertex set that leaves $4$ components), but we don't try to measure ratios yet: we consider a $7$-vertex set that leaves $4$ components to be incomparable to a $6$-vertex set that leaves $3$ components. In other words, we are finding all the sets on the "Pareto frontier" of the size/number-of-components tradeoff. (One candidate set is always the empty set; it is the best set of its size!)

Then, we collect all the sets we found under all the hypotheses into a single family $\mathcal F$. Lots of sets are repeated with different hypothesis, which helps keep $\mathcal F$ small; when I did this, I got $|\mathcal F| = 53$, but I did not fully eliminate suboptimal sets, so this could get even smaller.

The reason we're doing this is that, in the overall Tutte graph, the optimal cut-set that achieves the toughness must intersect each "third" of the graph in a set from $\mathcal F$. This leaves us with only $2|\mathcal F|^3$ cases to check: From each third of the graph, we select a set corresponding to some set from $\mathcal F$, and also we either do or don't delete the center vertex.

$2|\mathcal F|^3$ is small enough to handle by brute force! Excluding the cases that are not cut-sets, I found six optimal sets all achieving a toughness of $\frac87$, as in the diagram at the beginning of this answer.