0

Suppose a bivariate probability distribution is continuous and has circular symmetry about the origin; i.e., the lines of constant density are concentric circles centered on the origin.

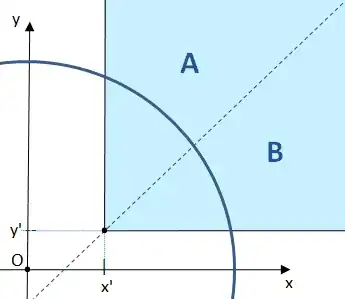
Now consider the "shifted quadrant" $Q(x',y'):=\{(x,y)\in\Bbb R^2: x>x', y>y'\}$, bisected by its "diagonal" through point $(x',y')$, and let $A$ (resp. $B$) denote the half of this quadrant that's above (resp. below) the bisector. Here's a picture, including a circular line of constant density:

bisection of shifted quadrant

The picture happens to show the case $x'>y'$, where it's obvious that every circle of constant density has a longer segment in $A$ than in $B$. Similarly, when $x'<y'$ the longer segment is in $B$, and when $x'=y'$ the segments have equal length.

Are these facts sufficient to establish the following? (Or, if not, how can it be proved more rigorously?) ...

Claim: If a bivariate distribution is continuous and has circular symmetry about the origin, then $\ \ x' \lesseqqgtr y'\implies P(A) \lesseqqgtr P(B).$

Since $P(A)+P(B)=P(Q),$ the conclusion can also be written as $$x' \lesseqqgtr y'\implies P(A)\lesseqqgtr{1\over2}P(Q)\implies P(B)\gtreqqless{1\over2}P(Q)$$ or $$x' \lesseqqgtr y'\implies P(A\mid Q)\lesseqqgtr{1\over2}\implies P(B\mid Q)\gtreqqless{1\over2}$$

Note: This claim is relevant to completing a proof that $P(Y+b>X\mid X>c,Y>c)$ is monotone increasing in $c$, when $X,Y$ are i.i.d. Normal with mean $0$.

r.e.s.
  • 15,537

1 Answers1

1

It is sort of sufficient.

Edited details:

Let $f(x,y)$ be the density and $C_n = \{(x,y): x^2+y^2 \le n\}$. Define $$I_n := \int_{A\cap C_n} f(x,y) \mathrm{dx} \mathrm{dy}~,\quad J_n := \int_{B\cap C_n} f(x,y) \mathrm{dx} \mathrm{dy}~.$$ Then the problem asks to show $\lim_{n \to \infty} I_n \ge \lim_{n \to \infty} J_n$. Sufficient to show that $I_n \ge J_n~ \forall n$. Further define $$I_n^+(\delta) := \sum_{i = K_0}^K \max_{(x,y) \in A_i} f(x,y) \Delta(A_i)~, \quad J_n^+(\delta) := \sum_{i = K_0}^K \max_{(x,y) \in A_i} f(x,y) \Delta(B_i)~, \quad \text{where}$$ \begin{align*} A_i &:= \{(x,y) \in A\cap C_n:i\delta \le x^2+y^2 < (i+1)\delta\}~,\\ B_i &:= \{(x,y) \in B\cap C_n:i\delta \le x^2+y^2 < (i+1)\delta\}~, \end{align*} $\Delta(S)$ being the area of a set $S$ and $K_0, K$ is suitably chosen to cover $A\cap C_n$ and $B\cap C_n$ (check why this is possible!). Since $I_n, J_n$ exist, $$\lim_{\delta \to 0}I_n^+(\delta) = I_n~, \quad \lim_{\delta \to 0}J_n^+(\delta) = J_n~.$$

By property of $f$ and construction of the partition, $$\max_{(x,y) \in A_i} f(x,y)=\max_{(x,y) \in B_i} f(x,y)~.$$ Further, as mentioned in the OP, $\Delta(A_i) \ge \Delta (B_i)$, which gives $I_n^+(\delta)\ge J_n^+(\delta)$. Thus, $I_n \ge J_n$.

Sounak
  • 179