1

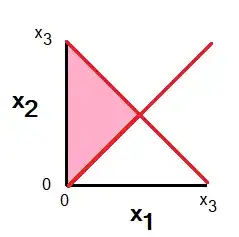
I am working on a problem involving order statistics and I'm having trouble determining the bounds of integration when multiple inequalities are involved. Here is the specific integral I'm trying to evaluate:

$$ \int \int \int 3! \cdot 1_{[0 \leq x_1 \leq x_2 \leq x_3 \leq 1]} \cdot 1_{[x_1 + x_2 < x_3]} dx_1 dx_2 dx_3 $$

I understand the concept of order statistics, but I am unsure how to set up the bounds for integral based on the given inequalities. Could someone explain how to find the correct region of integration for these types of problems?

Here are my specific questions:

  • How do the inequalities translate into bounds for the variables ?
  • Is there a systematic way to approach setting up these bounds when dealing with multiple inequalities ?

Any detailed explanation or step-by-step guidance would be greatly appreciated.

Thank you!

RobPratt
  • 50,938
Gliph182
  • 11
  • Related (same underlying question but different methods): https://math.stackexchange.com/questions/253893/probability-that-three-independent-uniform-0-1-random-variables-can-form-a-t and https://math.stackexchange.com/questions/146450/find-pzxy-where-x-y-z-sim-u0-1-independently – Henry Jul 17 '24 at 01:55
  • https://math.stackexchange.com/q/3140526/321264, https://math.stackexchange.com/q/2033347/321264 – StubbornAtom Jul 17 '24 at 14:26

1 Answers1

1

You have various constraints. Treating $x_3$ as fixed for a moment, the area you are integrating over for $x_1$ and $x_2$ looks like

diagram

Since you seem to want to integrate with respect to $x_1$ first, then $x_2$, then $x_3$, one approach would be

  • to start with $0 \le x_1 \le x_2$ and $x_1+x_2 < x_3$ $($i.e. $x_1 < x_3-x_2$) so use $\int\limits_{x_1=0}^{\min(x_2,x_3-x_2)}\cdots dx_1$ to deal with $x_1$
  • then $0 \le x_2 \le x_3$ so use $\int\limits_{x_2=0}^{x_3}\cdots dx_2 $ to deal with $x_2$
  • then $0 \le x_3 \le 1$ so use $\int\limits_{x_3=0}^{1}\cdots dx_3$ to deal with $x_3$

i.e. $$\int\limits_{x_3=0}^{1}\int\limits_{\,\,x_2=0}^{x_3}\int\limits_{x_1=0}^{\min(x_2,x_3-x_2)}\cdots \,dx_1 \, dx_2 \, dx_3$$

but the $\min(x_2,x_3-x_2)$ could cause complications so you might want to split this into cases where $0 \le x_2 \le \frac{x_3}2$ and where $\frac{x_3}2 \lt x_2 \le x_3$, so use

$$\int\limits_{x_3=0}^{1}\int\limits_{\,\,x_2=0\,\,}^{\frac{x_3}{2}}\int\limits_{x_1=0}^{x_2}\cdots dx_1 \, dx_2 \, dx_3 + \int\limits_{x_3=0}^{1}\int\limits_{\,x_2=\frac{x_3}{2}\,}^{x_3}\int\limits_{x_1=0}^{x_3-x_2}\cdots dx_1 \, dx_2 \, dx_3.$$

Henry
  • 169,616
  • Hi Henry. Thank you for the clear explanation. There was no particular reason why I wanted to integrate with respect to x_1 first. May I ask how you would have approached the problem? By that I mean, is there an integration order that is a lot easier? Intuitively, I would think by starting with x_3, since we have x_2 <= x_3 <= 1 and x_1 + x_2 <= x_3 <= 1 so we would use x_3 = max(x_2, x_1 + x_2) = x_2 + x_1 to x_3 = 1 as bounds. But then I get confused on which bounds to use for x_2 and x_1. – Gliph182 Jul 17 '24 at 01:33
  • @Gliph182 If you were to reverse the order of integration then I think you may want $$\int\limits_{x_1=0}^{1}\int\limits_{,,x_2=x_1,,}^{1}\int\limits_{x_3=\min(1,x_1+x_2)}^{1}\cdots ,dx_3 , dx_2 , dx_1$$ which may "simplify" to remove $\min$ to $$\int\limits_{x_1=0}^{\frac12}\int\limits_{,,x_2=x_1,,}^{1-x_1}\int\limits_{x_3=x_1+x_2}^{1}\cdots ,dx_3 , dx_2 , dx_1$$ – Henry Jul 17 '24 at 01:47