How to find the volume under this composite of functions?

Question

I am trying to get the average height of a surface composed of multiple functions, but my limited understanding of Calculus is keeping me from doing so.

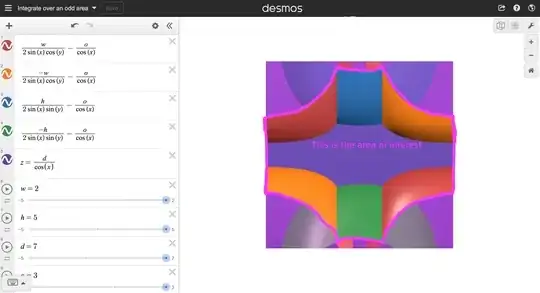
I am interested in integrating over the minimum of all the separate functions, essentially taking the double integral of some sort of minimum composite function. What I think is the harder problem, however, is defining this integral with the weird bounds. I want to integrate over well defined ranges of x and y (for the sake of a placeholder, lets say $\{x|-\frac{\pi}{4}\leq x \leq \frac{\pi}{4}\}$ and $\{ y | 0\leq y \leq \pi \}$), but I also want to confine the area to a not-so-easily-defined region as well. As you can see in the above image, the area of interest has many curved edges. These curved are defined by the intersections of the constituent functions and $z = 0$ plane. Finally, of course, I would like to get the average height of the area of interest (an easier problem, but one I am yet unable to solve).

Here is a Desmos demonstration of the full problem.

If any Calculus pros could help me through this interesting problem, I would greatly appreciate it.

TL;DR: How do I find the integral of the area of interest defined in the screenshot above?

Edit:

Are you asking about the area of the surface =min {1(,),…5(,)} within the pink boundary, or as the bird's-eye view suggests, the area of the 2D shape with the pink boundary?

The area of the 2D shape with the pink boundary. As the double integral projects down onto the plane, however, it's kind of both at the same time. I'm really asking about the volume between =min {1(,),…5(,)} and the 2D shape with the pink boundary.

Answer 1

Denote the region of interest by $D$. Judging by the given plot range, which cuts off the surfaces from below in the plane $z=0$, $D$ is the region with boundary consisting of the curves

$$\begin{cases} \tan x \cos y = \pm \dfrac w{2o} \\ \tan x\sin y = \pm \dfrac h{2o} \end{cases}$$

obtained by setting $z=f(x,y)=0$ in the first four equations and condensing terms. Thus consider substituting

$$(u,v)=(\tan x\cos y, \tan x\sin y) \iff (x,y) = \left(\arctan\sqrt{u^2+v^2}, \arctan \frac vu\right)$$

to transform $D$ to the rectangle $D' := \left[-\dfrac w{2o},\dfrac w{2o}\right]\times\left[-\dfrac h{2o},\dfrac h{2o}\right]$. The integral for the area $A$ is

$$A = \iint_D dx \, dy = \iint_{D'} \frac{du\,dv}{\sqrt{u^2+v^2} \left(1+u^2+v^2\right)}$$

and by symmetry, we have

$$A = 4 \int_0^{\tfrac h{2o}} \int_0^\tfrac w{2o} \frac{du\,dv}{\sqrt{u^2+v^2} \left(1+u^2+v^2\right)}$$

So an integral for the area has been found. Evaluating it and recovering a closed form is the tricky part. For instance, upon fixing $w,h,o$ so the upper integration limits reduce to $1$, the exact value is quite hairy; see this Wolfram cloud notebook.

---

As for the volume, we of course have

$$V = \iint_D \left(\int_0^{F(x,y)} dz\right) \, dx \, dy$$

where $F(x,y)$ is the minimum of the five given surfaces. Thanks to symmetry, we need only consider the quadrant of $D$ where $(x,y)\in\left[0,\dfrac\pi4\right]\times\left[0,\dfrac\pi2\right]$, covered by the red, blue, and purple surfaces. Denote the subsets of $D$ directly below each of these surfaces by $D_r,D_b,D_p$, resp. The surfaces intersect along the curves

• $w \tan y = h$ (red-blue)
• $w \sec y = 2 (d+o) \tan x$ (red-purple)
• $h \csc y = 2 (d+o) \tan x$ (blue-purple)

The area integrals over these subsets of $D$ are

$$\begin{align*} \iint_{D_r} dA &= \int_{y=0}^{\arctan\tfrac hw} \int_{x=\arctan\tfrac{w\sec y}{2(d+o)}}^{\arctan\tfrac{w\sec y}{2o}} dx \, dy \\[1ex] \iint_{D_b} dA &= \int_{y=\arctan\tfrac hw}^\tfrac\pi2 \int_{x=\arctan\tfrac{h\csc y}{2(d+o)}}^{\arctan\tfrac{h\csc y}{2o}} dx \, dy \\[1ex] \iint_{D_p} dA &= \left\{\int_{y=0}^{\arctan\tfrac hw} \int_{x=0}^{\arctan\tfrac{w\sec y}{2(d+o)}} + \int_{y=\arctan\tfrac hw}^\tfrac\pi2 \int_{x=0}^{\arctan\tfrac{h\csc y}{2(d+o)}} \right\} dx \, dy \end{align*}$$

so that the total volume integral would be

$$V = 4 \left\{\iint_{D_r} \int_{z=0}^{\tfrac w{2\sin x\cos y}-\tfrac o{\cos x}} + \iint_{D_b} \int_{z=0}^{\tfrac h{2\sin x\sin y} - \tfrac o{\cos x}} + \iint_{D_p} \int_{z=0}^{z=\tfrac d{\cos x}}\right\} dz \, dx \, dy$$