For info on tens of thousands of triangle centers, consult Clark Kimberling's Encyclopedia of Triangle Centers; in particular, the orthocenter entry $X(4)$ gives the following barycentric coordinates:
$$u:v:w =\frac1{-a^2+b^2+c^2}:\frac1{-b^2+c^2+a^2}:\frac1{-c^2+a^2+b^2}$$ (As the components involve squares of side-lengths, it's straightforward to re-write them in terms of $(x_i,y_i)$.) These allow you to express the coordinates of the orthocenter as a weighted average of the coordinates of the vertices:
$$\frac{uA+vB+wC}{u+v+w}$$
As a user of GeoGebra, OP should be pleased to know of the app's built-in support for this stuff via the command TriangleCenter(A, B, C, n), where n is the ETC index (incenter, $n=1$; centroid, $n=2$; circumcenter, $n=3$; orthocenter, $n=4$; nine-point center, $n=5$; etc, etc, ETC ...). I believe GeoGebra currently supports up to just-over $n=3000$; I actually used the feature to search for centers that could answer this question, finding $n=1138$ as a result.
(You can also have GeoGebra calculate barycentric $u$-$v$-$w$ coordinates individually, and then define the corresponding point as (u A + v B + w C)/(u + v + w). I have to do that from time to time.)
Mathematica also has a TriangleCenter[tri, type] function, but (a little surprisingly) it supports only a few named types. As Orthocenter is supported, the app can generate an explicit coordinate formula for you:
Factor[TriangleCenter[{{x1, y1}, {x2, y2}, {x3, y3}}, "Orthocenter"]] yields:
{-(x1 x2 y1 - x1 x3 y1 - x1 x2 y2 + x2 x3 y2 + y1^2 y2 - y1 y2^2 + x1 x3 y3 - x2 x3 y3 - y1^2 y3 + y2^2 y3 + y1 y3^2 - y2 y3^2)/(-x2 y1 + x3 y1 + x1 y2 - x3 y2 - x1 y3 + x2 y3), ( x1^2 x2 - x1 x2^2 - x1^2 x3 + x2^2 x3 + x1 x3^2 - x2 x3^2 + x1 y1 y2 - x2 y1 y2 - x1 y1 y3 + x3 y1 y3 + x2 y2 y3 - x3 y2 y3)/(- x2 y1 + x3 y1 + x1 y2 - x3 y2 - x1 y3 + x2 y3)}
which is a bit of a mess. With a bit of effort, cleverness, and luck, you could re-arrange the above into the form
{x1,y1} p/s + {x2,y2} q/s + {x3,y3} r/s
where expressions p, q, r are obtained from each other by cycling elements: x1$\to$x2$\to$x3$\to$x1 and y1$\to$y2$\to$y3$\to$y1, and s is fully-symmetric. As it happens, p/s, q/s, r/s (with s = p+q+r) are equivalent to the $u$-$v$-$w$ expressions above, with lengths expanded using Cartesian-coordinates.
This highlights another benefit of barycentric coordinates (and similar representations): notational tidiness.
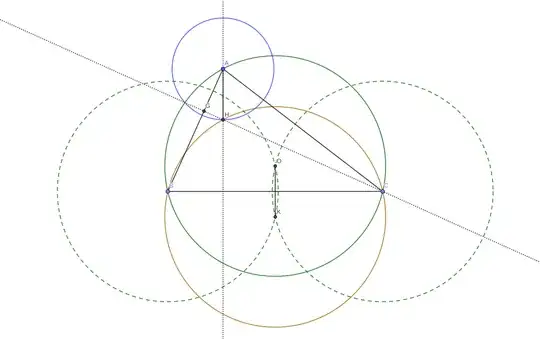
Slope of $AB$ and $AC$ are respectively $m_1=\dfrac{b_2-a_2}{b_1-a_1}$ and $m_2=\dfrac{c_2-a_2}{c_1-a_1}$ so the orthocenter is given by the system $$\begin{cases}y-c_2=\frac{-1}{m_1}(x-c_1)\y-b_2=\frac{-1}{m_2}(x-b_1)\end{cases}$$ (it is not necessary to take the height passing by $A$ because you know why).
– Ataulfo Jul 09 '24 at 22:51