What is the maximum of $ \frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)}$?

Question

We know the global maxima of the function $\frac{\sin(nx)}{\sin(x)}$ is $n$ (thanks to this question), but

what is the global maxima of $\frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)}, \text{ where $a$ is a constant term?}$

Background: It represents the intensity of a narrow-slit diffraction grating but in a more specific application.

Attached is a plot of the maximum absolute value vs $a$ for different $N$. There definitely seems to be an expression which relates the maxima, $a$, and $N$.

and the MATLAB code used to produce the results of above image:

N = 40;
x = -pi/2:0.001:pi/2;
a = -pi/2:0.01:pi/2;
% figure;
for i = 1:length(a)
    y = sin(N(x + a(i)))./sin(x+a(i)) + sin(N(x - a(i)))./sin(x-a(i));

    temp(i) = max(abs(y));
    % hold on;plot(x,y);
end
figure;plot(a,temp)

Edit: Here is a link to the desmos graph

Answer 1

Discussion on the special case in @user64494's answer.

The maximum of $$f(x) := \frac{\sin 4(x + 1)}{\sin(x + 1)} + \frac{\sin 4(x - 1)}{\sin(x - 1)}$$ is given by $$f_{\max} = \frac{8\sqrt{6}}{9} (2 - 3\cos 2)\cos 1\, \sqrt{\frac{2 - 3\cos 2}{1 - 2\cos 2}}$$ when e.g. $$x = \arccos \sqrt{- \frac{(2 - 3\cos 2)\cos 1}{6\cos 3}}.$$

Here we just compare my result with @user64494's. The first 500 digits of them are the same (I only input 500).

Answer 2

Based on the plots I have shown in the question, it seems the below equation gives an approximation of the maximum$$N + \frac{sin(2Na)}{sin(2a)}$$ .

The cyan colored plots are plots of the above equation while the red, blue and black plots are obtained by finding the maximum programmatically.

Of course, I still don't know why this is the case. Hopefully this helps us in finding/proving the expression for maximum.

Answer 3

1. Question Restatement to Reference its Equations and Link

We know the global maxima of the function $$f\left(n,x\right) =\frac{\sin(nx)}{\sin(x)} \text{ is } n $$ $$\tag{Eq. 1.1}$$ (thanks to this question), but what is the global maxima of $$g\left(n,a,x\right) =\frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)}, \text{ where $a$ is a constant term?}$$ $$\tag{Eq. 1.2}$$

Not stated directly, but instead by the linked reference, of course $n \in \{\text{Set of Integers}\}$ and $n>0$. The $n$ positive integer requirement results in a finite series in the answer.

Notice that $g(n,a,-x)=\frac{\sin(n(-x+a))}{\sin(-x+a)} + \frac{\sin(n(-x-a))}{\sin(-x-a)}= \frac{\sin(n(-x+a))}{\sin(-x+a)} + \frac{\sin(n(x+a))}{\sin(x+a)}$ $= \frac{\sin(n(x-a))}{\sin(x-a)} + \frac{\sin(n(x+a))}{\sin(x+a)}$, so that $g(n,a,x)=g(n,a,-x)$ and $g$ is an even function of $x$. That means that locally $g$ can be expanded as an even Taylor series in $x$, being $g(n,a,x)\approx g_0+g_1\,x+g_2\,x^2+...$. But since $g$ is even in $x$ then $g_1\to 0$ and only $g(n,a,x)\approx g_0+g_2\,x^2+...$ with a local minimum or maximum at $x=0$.

2. Solution Steps

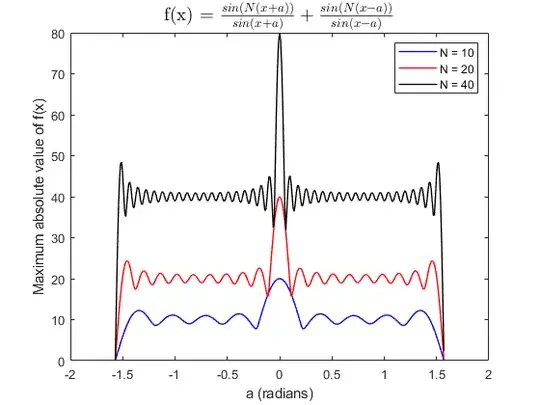
All of the graphs show that a maximum occurs at $x=0$. But why?

From the article Prove that $\sin n\theta=n\sin \theta-\frac{n(n^2-1)}{3!}\sin^3\theta+\frac{n(n^2-1)(n^2-3^2)}{5!}\sin^5\theta+\cdots$. From the answer given by Paramanand Singh is quoted:

$$\sin n\theta = n\sin \theta - \frac{n(n^{2} - 1^{2})}{3!}\sin^{3}\theta + \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{5}\theta - \cdots\tag{2}$$

Thus for $\sin n\theta$ all terms are divisible by $\sin \theta$, even in the limit that $\theta \to 0$ but not of course for $\theta=0$. Now the quantity $\frac{\sin n \theta}{\sin \theta}$ can be calculated: $$\frac{\sin n \theta}{\sin \theta} =n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\theta + \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\theta - \cdots$$ Similarly, $$\frac{\sin n \left(x+a\right)}{\sin \left(x+a\right)} =n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x+a\right) + \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\left(x+a\right) - \cdots$$ And, $$\frac{\sin n \left(x-a\right)}{\sin \left(x-a\right)} =n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x-a\right) + \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\left(x-a\right) - \cdots$$ So, $$ \frac{\sin n \left(x+a\right)}{\sin \left(x+a\right)}+ \frac{\sin n \left(x-a\right)}{\sin \left(x-a\right)} = n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x+a\right) + \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\left(x+a\right) - \cdots \\+ n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x-a\right) + \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\left(x-a\right) - \cdots $$ $$\tag{Eq. 2.2}$$ Now evaluate the derivative of the quantity $sin^{2\,m}\left(x+a\right)+sin^{2\,m}\left(x-a\right)$ at $x \to 0$ using the Taylor Series Expansion for $\sin\left(y\right) \to y-\frac1{6}y^3+...$ : $$\left.\frac{d}{d\,x} \left( sin^{2\,m}\left(x+a\right)+sin^{2\,m}\left(x-a\right) \right)\right|_{x\to 0} =$$ $$\to \left. \left( n \left(x+a\right)^{2\,m-1}+\left(\text{Higher Order Terms of x}\right)+ n \left(x-a\right)^{2\,m-1}+\left(\text{Higher Order Terms of x}\right) \right)\right|_{x\to 0}$$ Given that $2m-1$ is always odd then *the terms in $a$ cancel in the limit $x\to 0$, resulting in a maximum there since $n>0$ and it is an integer. This is the same result as in the graphs which all show the global maximum at $x=0$. Note that both $\sin\left(n\,x\right)$ and $\sin\left(x\right)$ over a period of $x \to q\,2\pi$, where $q$ is some arbitrary integer. However, the global maximum value itself does not change.

The maximum is simply $g_{maxiumum}=g |_{x=0}$:

$$g\left(n,a,x\right)_{maximum} =\left.\left( \frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)} \right)\right|_{maximum\,x\to 0}$$

The maximum is given by:

$$ \boxed{g\left(n,a,x\right)_{maximum} \to \left.\left( \frac{\sin(n(a))}{\sin(+a)} + \frac{\sin(n(-a))}{\sin(-a)} \right)\right|_{maximum\,x\to 0} \to \left. \left(2\,\frac{\sin(n(a))}{\sin(a)}\right)\right|_{maximum\,x\to 0} } $$ Note: that this result was referencing the graphs in the question that all had local maxima at $x=0$. A local minimum is also possible at $x=0$.

3. Example plot of $ y=\frac{\sin\left(4\cdot\left(x+1\right)\right)}{x+1}+\frac{\sin\left(4\cdot\left(x-1\right)\right)}{x-1} $with $n=4$ and $a=1$

In the comments section, there is a link to the plot of $$ y=\frac{\sin\left(4\cdot\left(x+1\right)\right)}{x+1}+\frac{\sin\left(4\cdot\left(x-1\right)\right)}{x-1} $$ The Desmos plots of the same equations show a difference as pictured (and quoted) below:

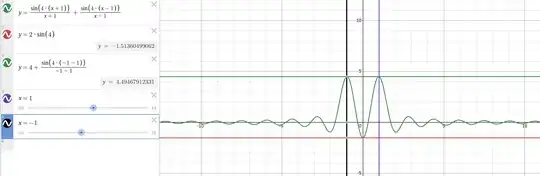
Looking at the equations within the above plot, it is easy to see what is happening. The function $g$ is at a minimum at $x=0$. In this case there are two maxima, one at $g=a$ and the other at $g=-a$. Plugging either of these and taking the appropriate limit results in the maximum for $g$ just like the equations in the linked plot. Comparing the result for $g$ between $x=0$ and $x=a$ allows for determining the absolute maximum.

4. Maxima Discussion for $y=g\left(n=6,a=1.5,x\right)_{maximum} =\left.\left( \frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)} \right)\right|_{n=6,a=1.5} $

When $n>0$ as in this case, then the maximum or maxima are positive. Also, since $g(n,a,x)$ is an even function, then for the purposes of calculating the second derivative $g(n,a,x)$ can be approximated as a Taylor series (where $g_1=0$ since g is an even function) for the first powers of $x$ as: $$g(n,a,x)\approx g_0 + g_2\,x^2+\,\text{Higher order powers of x}$$ $$\tag{Eq. 4.1}$$ which according to Equation 2.2 is: $$ \begin{align} \frac{\sin n \left(x+a\right)}{\sin \left(x+a\right)}+ \frac{\sin n \left(x-a\right)}{\sin \left(x-a\right)} &=\\ &= n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x+a\right) + \\ &+ \frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\left(x+a\right) - \cdots +\\&+ n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x-a\right) + \\ &+\frac{n(n^{2} - 1^{2})(n^{2} - 3^{2})}{5!}\sin^{4}\left(x-a\right) - \cdots \end{align} $$ $$\tag{Quoted Eq. 2.2}$$ Applying the Taylor expansion for $\sin x \approx x +\, \text{Higher order terms of $x$}\, $ then: $$ \begin{align} \frac{\sin n \left(x+a\right)}{\sin \left(x+a\right)}+ \frac{\sin n \left(x-a\right)}{\sin \left(x-a\right)} &\approx\\ &\approx n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x+a\right) +\cdots \\ &+ n - \frac{n(n^{2} - 1^{2})}{3!}\sin^{2}\left(x-a\right) +\cdots \\ \end{align} $$ $$\tag{4.2}$$ $$ \frac{\sin n \left(x+a\right)}{\sin \left(x+a\right)}+ \frac{\sin n \left(x-a\right)}{\sin \left(x-a\right)} \approx n - \frac{n(n^{2} - 1^{2})}{3!}\left(x+a\right)^2 +\cdots + n - \frac{n(n^{2} - 1^{2})}{3!}\left(x-a\right)^2 +\cdots \\ \approx 2\,n-2\,\frac{n(n^{2} - 1^{2})}{3!}\left(x^2+a^2\right)+\cdots $$ $$ \begin{align} \frac{d^2}{d\,x^2}\left.\left( \frac{\sin n \left(x+a\right)}{\sin \left(x+a\right)}+ \frac{\sin n \left(x-a\right)}{\sin \left(x-a\right)} \right)\right|_{x \to 0} &\approx \frac{d^2}{d\,x^2}\left. \left( 2\,n-2\,\frac{n(n^{2} - 1^{2})}{3!}\left(x^2+a^2\right)+\cdots \right)\right|_{x\to 0} \\ &\approx \left. \left( -2\frac{n(n^{2} - 1^{2})}{3!}\left(1\right)+\cdots \right)\right|_{x\to 0} \end{align}$$ $$\tag{Eqs. 4.3}$$ When the second derivative in Equation 4.3 is negative, then there is a local maximum at $x=0$ since in this case $g_2$ in Equation 4.1 $g(n,a,x)\approx g_0 + g_2\,x^2+\,\text{Higher order powers of x}$ is negative, indicating locally around $x\to 0$ an upside down parabola. The other case, occurs when there is a local minimum at $x=0$, in which case there are two maxima for $g(n,a,x)$, each of equal value since $g(n,a,x)$ is an even function of $x$.

Thus the result is to calculate two values, and take the maximum of the two of them to be the global maximum for $n > 0$ of course. Because all of the minima of $\frac{sin n\,x}{x}$ are less in magnitude than $n$, the maxima (if two) for $g(n,a,x)$ are always positive as for $g(n,a,x=0)$.

5. Maxima Calculation for $y=g\left(n=6,a=1.5,x\right)_{maximum} =\left.\left( \frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)} \right)\right|_{n=6,a=1.5} $

Consider now the problem referenced in the comments section: $$g\left(n=6,a=1.5,x\right) =\frac{\sin(6\cdot (x+1.5))}{\sin(x+1.5)} + \frac{\sin(6\cdot (x-1.5))}{\sin(x-1.5)}$$ $$\tag{Eq. 5.1}$$ To determine the global maximum, $g(6,1.5,x)$ needs to be evaluated at two limits, $x\to 0$ and $x\to 1.5$ to find for which of these limits $g(6,1.5,x)$ is a global maximum. Of course, if $g(6,1.5,x)$ turns out to be the maximum between the two, then because $g$ is an even function of $x$, then there are actually two maxima, each of equal value, namely $g_{maximum\,1}=g_{maximum\,2}=g(6,1.5,x)\lim_{x\to 1.5}$. Hence, Equation 5.1 is first evaluated (using $sin()$ with $()$ being Radians) for the limit $x\to 0$: $$g_1\left(n=6,a=1.5,x \to 0\right) =\left. \frac{\sin(6\cdot (x+1.5))}{\sin(x+1.5)} + \frac{\sin(6\cdot (x-1.5))}{\sin(x-1.5)}\right|_{\lim x \to 0}=$$ $$ =\frac{\sin(6\cdot (1.5))}{\sin(1.5)} + \frac{\sin(6\cdot (-1.5))}{\sin(-1.5)}=0.549 \, \text{from the Desmos online calculator} $$ $$g_2\left(n=6,a=1.5,x \to 1.5\right) =\left. \frac{\sin(6\cdot (x+1.5))}{\sin(x+1.5)} + \frac{\sin(6\cdot (x-1.5))}{\sin(x-1.5)}\right|_{\lim x \to 1.5}=$$ $$ =\frac{\sin(6\cdot (3))}{\sin(3)} + 6=5.749670917743 \,\,\text{And $g_2=5.749670917743$ is the expected }\textbf{maximum}. $$ $$\tag{Eqs. 5.2}$$

6. Plots for $y=g\left(n=6,a=1.5,x\right)_{maximum} =\left.\left( \frac{\sin(n(x+a))}{\sin(x+a)} + \frac{\sin(n(x-a))}{\sin(x-a)} \right)\right|_{n=6,a=1.5} $

Consider now the problem referenced in the comments section: $$g\left(n=6,a=1.5,x\right) =\frac{\sin(6\cdot (x+1.5))}{\sin(x+1.5)} + \frac{\sin(6\cdot (x-1.5))}{\sin(x-1.5)}$$ $$\tag{Reference to Eq. 5.1}$$ Let $g\to y$ and plot it accordingly in two dimensions using the Desmos plotter resulting in the following quoted plot:

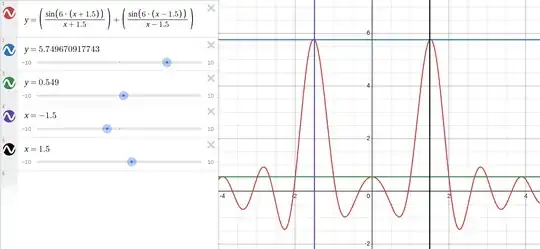
The equations used in the above plot were as follows: $$ y=\left(\frac{\sin\left(6\cdot\left(x+1.5\right)\right)}{x+1.5}\right)+\left(\frac{\sin\left(6\cdot\left(x-1.5\right)\right)}{x-1.5}\right)\\ y=5.749670917743\,\text{ , }\, y=0.549\,\text{ , }\, x=-1.5\,\text{ , and }\, x=+1.5 $$ $$\tag{Eqs. 5.1}$$

As can be seen, the results are as expected, with $y_{maximum}=5.749670917743$ which occurs at $x=-1.5$ and also the same value at $x=1.5$. Also, at $x=0$ there is a local maximum of $y_{x=0}=0.549$, but this is not a global maximum. That is why the two values need to be compared to arrive at the final result.