0

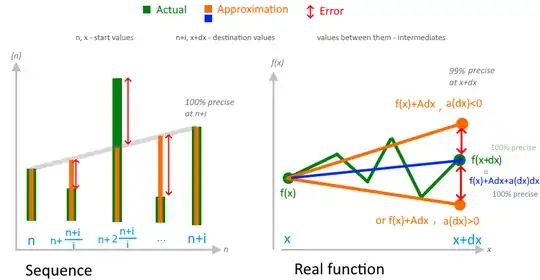
Sequence

If we consider a sequence, we can find how any next element is changed relatively to the given as $\{n+1\}-\{n\}$.

We can also find how every given + $i$, element is different from the given, i.e. $\{n+i\}-\{n\}$, and if are infested of inspecting the difference only between $n+i$ and $n$ that's fine.

But, if, we want to find the difference between sequence elements, which indexes difference is lower than $i$, i.e. with higher "resolution", using $n+i$ equation, we can only use an approximation, for example, by dividing $\{n+i\}-\{n\}$ by $i$, and that will be a value that we will need to add to $n$th element $i$ times, to get exactly $n+i$ value, AND also approximate values of elements with indexes between $n$ and $n+i$.

In this case approximation means only that values of elements, with indexes between $n$ and $n+i$ may be wrong, right?

Real function

In case of real function, we find the difference between the values, which corresponding arguments values is infinitely small and then divide that difference between such values by infinitely small corresponding arguments difference (I do not really understand for what, since we consider it sort of the smallest undividable, but I have assumptions, so let me ask it in different question), getting same linear approximation, but now between $f(x)$ and $f(x+\delta x)$.

That means, that we divide the infinitely small function range ($\delta y$) by infinitely small argument difference ($\delta x$) parts (that may be greater than function difference, though) to know what value we should add to $f(x)$ $\delta x$ times to get $f(x+\delta x)$ value AND approximate values between them with $\delta x$ step.

The question

The problem is that $\lim_{\delta x->0} \dfrac{f(x+\delta x)-f(x)}{\delta x}=\lim_{\delta x -> 0}(A + \alpha(\delta x))=A$, where $\alpha(\delta x)$ is infinitely small at $\delta x->0$, and then

$$f(x+\delta x) = f(x) + A\delta x + \fbox{α(δx)δx}$$

Do I understand correctly, that in case of derivative, by approximation it means that, unlike the sequences, where $n+i$ will be 100% precise and between $n$ and $n+i$ may be wrong, for real function, values between $f(x + \delta x)$ and $f(x)$ are also may be wrong, but the destination value $f(x + \delta x)$ will be wrong too on $α(δx)δx$ (smaller or greater), which is, however infinitely small, so the error is infinitely small, and the correctness is infinitely close to 100%, yet not 100%?

enter image description here

isagsadvb
  • 91
  • 1
    There is no such thing as "infinitely small". This may help: https://math.stackexchange.com/questions/4568242/using-calculus-notation-arithmetically/4568253#4568253 – Ethan Bolker Jun 26 '24 at 11:21
  • @EthanBolker, an infinitely small at $x->x_0$is a real function $\alpha(x)$ such that $\lim_{x->x_0}\alpha(x)=0$, but I will read what You provided anyway – isagsadvb Jun 26 '24 at 11:35
  • I can write a more substantial answer, but what is meant is that the derivative $f'(x)$ is the unique linear transformation (in the $\mathbb{R}^1 \to \mathbb{R}^1$ case we think of it as just a number) such that $f(x + h) = f(x) + f'(x)h + r(h)$ for some $r(h)$ such that $\lim_{h \to 0} \frac{r(h)}{h} = 0$. That is, $f(x + h)$ is $f(x) + f'(x) + h$ up to a remainder that dies faster than $h$ as $h$ gets close to $0$. You can prove that there can only be one linear transformation with this property at a point for a given function. – Charles Hudgins Jun 26 '24 at 11:41
  • @CharlesHudgins, why $f'(x)h+r(h)$ instead of $f'(x)h+r(h)h$? Just from definition that it is already infinitely small, "little-o" in particularly? – isagsadvb Jun 26 '24 at 12:22
  • I have a typo in my comment. It should read "$f(x + h)$ is $f(x) + f'(x)h$ up to a remainder that dies faster than $h$ as $h$ gets close to $0$." In any case, we don't write it as you say because the point of the $r(h)$ term is to be an "error" term. The idea is that the derivative is the best linear approximation at a point. What do we mean by best? We mean that it's only off by an error term $r(h)$ that gets small faster than $h$ as $h$ gets small. – Charles Hudgins Jun 26 '24 at 12:27
  • @CharlesHudgins, I think I got a bit confused. If to look on the illustration I provided, I thought, that a(dx)dx is an extra, that makes an error, but actually it seems to be vice-versa a fix, with that function should be 100% correct at $x+dx$. And if we consider only $f(x)+f'(x)dx$ as You wrote it will have an error a(dx)dx, and, probably at the same time I thought that this monomial always is reduce unlike the $f'(x)dx$, during taking the limit, however, they are reduced both – isagsadvb Jun 26 '24 at 12:32
  • @CharlesHudgins, 1) seems like I was originally correct, but confused myself with wrong illustration. I updated the post and also answered myself, I would appreciate if You check. 2) As for my initial comment, I asked, why did You write $f(x+h)=f(x)+f′(x)h+r(h)$ instead of $f(x+h)=f(x)+f′(x)h+r(h)h$ – isagsadvb Jun 28 '24 at 11:12

1 Answers1

1

Seems like I was initially right, but then confused myself, while drawing wrong illustration, and attached to my post. Now it is correct, and seems the initial idea was correct.

There is a theorem called "Theorem about the relationship between a function, its limit at a limit point, and an infinitely small at a limit point", that I, for some reason can find only in Russian-language literature, for example here (theorem 17.5):

Function $f(x) $ has a finite limit $A$ at a limit point $x_0 \in D(f)$, if the function can be represented as a sum of value $A$ and an infinitely small at $x_0$:

$$\exists \lim_{x-x_0}f(x)=A <=> f(x)=A+\alpha_{x-x_0}(x)$$

An infinitely small at $x−>x_0$ is a real function $α(x)$ such that $\lim_{x−>x_0}α(x)=0$.

According to that, function $f(x)$ is differentiable (again, Russian Wikipedia) at $x_0$, i.e. has derivative value $A=f'(x)$ if:

$$\exists \lim_{\delta x-0}\dfrac{f(x+\delta x)-f(x)}{\delta x}=A=f'(x) <=> \dfrac{f(x+\delta x)-f(x)}{\delta x}=A+\alpha_{\delta x-0}(\delta x)=f'(x)+\alpha_{\delta x-0}(\delta x)$$

That means, that if we have $f(x)$, have its value in some $x_0$ and know $f'(x)$, we can find original $f(x_0+\delta x)$ value as $f(x_0)+\delta x(f'(x_0) + \alpha_{\delta x-0}(\delta x))$, and it will be 100% accurate original $f(x_0 + \delta x)$ value.

The problem, is that, when we take the limit $\lim_{\delta x-0}\dfrac{f(x+\delta x)-f(x)}{\delta x}$, if it exists we will get $\lim_{\delta x-0}f'(x)+\alpha_{\delta x-0}(\delta x)=f'(x)$, i.e. we lose $\alpha_{\delta x-0}(\delta x)$ part, and hence, if we next want to find $f(x + \delta x)$, we will add to it $(f'(x)*\delta x)$ and not $(f'(x)*\delta x + \alpha_{\delta x-0}(\delta x)*\delta x)$, that will be not accurate, as I shown on the illustration in the original post.

So, unlike the sequence average difference, i.e. velocity $\dfrac{\{n+i\}-\{n\}}{i}$, derivative not precise also for the final value, not only for intermediates.

If I missed something, please point me

isagsadvb
  • 91