Is the new series for a Big (or even Medium) Deal?

Question

There's been some oohing and ahhing in the science press recently over the discovery of a new formula for $\pi$ obtained as a side effect of computing amplitudes in string theory: $$\pi=4+\sum_{n=1}^\infty \frac1{n!}\left(\frac1{n+\lambda}-\frac4{2n+1}\right)\left(\frac{(2n+1)^2}{4(n+\lambda)}-n\right)_{n-1}$$

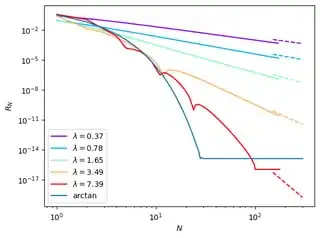
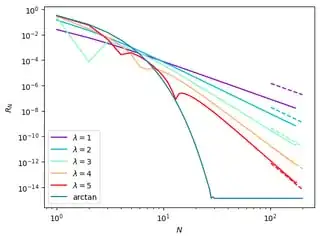
Here $(a)_b$ is the usual Pochammer symbol ($(a)_b=a(a+1)(a+2)\ldots(a+b-1)$) and $\lambda$ is a free parameter; in the large-$\lambda$ limit this becomes the classic Madhava-Leibniz formula $\pi=4\sum\frac{(-1)^n}{2n+1}$. The last term here is $\left(\frac{4(n-\lambda)+1}{4(n+\lambda)}\right)_{n-1}$; if I'm looking at it right then for large $n$ this is essentially the product of a term fairly close to $1$, a term of size roughly $\frac{2\lambda}{n+\lambda}$ (more specifically, $\frac{4(n-\lambda)-4(n+\lambda)+1}{4(n+\lambda)}$ $=\frac{1-8\lambda}{4(n+\lambda)}$), and then a set of terms coming to roughly $(n-3)!$. This would seem to suggest that the terms in the sum go as $\Theta(n^{-5})$ as $n\to\infty$: a factor of $\Theta(n^{-1})$ from the term in the first set of parentheses, a factor of $\Theta(n^{-1})$ from the $\approx\frac{2\lambda}{n+\lambda}$ term, and then a factor of $\Theta(n^{-3})$ from the $\frac{\approx(n-3)!}{n!}$ piece. That would suggest that this series converges quickly but not nearly so quickly as the various series with terms of order $c^{-n}$ that give a number of digits linearly proportional to the number of terms.

My questions are then basically: (1) Is my analysis roughly correct here, do I have the right order on terms? and (2) if not (or if so, I suppose) is this in fact a practical or competitive way to compute $\pi$? As a sort of secondary question, this formula bears at least a passing resemblance to the sort of term one might get by applying the Euler transformation to a different alternating series; is it possible that this is a transform of a known series?

Answer 1

Too long for a comment.

Going from Pochhammer symbols to the gamma function, the summand is $$a_{n,\lambda}=-\frac{(2n+4 \lambda -1)\,\, \Gamma \left(\frac{4 n^2-4 \lambda +1}{4 (n+\lambda )}\right)}{(2 n+1) (n+\lambda ) \,\,\Gamma (n+1)\,\, \Gamma \left(\frac{1-4 n (\lambda -1)}{4 (n+\lambda )}\right)}$$

$$\frac{a_{n+1,\lambda}}{a_{n,\lambda}}=1-\frac{\lambda +2}{n}-\frac{(2 \lambda -1)^2 \log (n)-\alpha}{4 n^2}$$ where $$\alpha=4 \lambda ^2+(2 \lambda-1 )^2\,\psi ^{(0)}(1-\lambda )+17$$

Adding $10,000$ terms for various $\lambda$, some numbers $$\left( \begin{array}{cc} \lambda & 4+\sum_{n=1}^{10^4} a_n \\ 0 & \color{red}{3.14169265}6449014122789803 \\ 1 & \color{red}{3.141592653589}876574977781 \\ 2 & \color{red}{3.141592653589793}182123845 \\ 3 & \color{red}{3.1415926535897932384}87758 \\ 4 & \color{red}{3.1415926535897932384626}31 \\ 5 & \color{red}{3.141592653589793238462643} \\ \end{array} \right)$$

while, for the same number of terms, Madhava-Leibniz formula gives $\color{red}{3.141}6926436$.

Using the same number of terms, for $\lambda=10$, the absolute error is $2.91\times 10^{-42}$ and, for $\lambda=100$, it drops to $3.92\times 10^{-250}$ and for $\lambda=1000$ it is less than $1.00\times 10^{-1000}$.

Answer 2

You can compute an asymptotic equivalent of the sum's terms: $$ u_n(\lambda) = \frac1{n!}\left(\frac1{n+\lambda}-\frac4{2n+1}\right)\left(\frac{(2n+1)^2}{4(n+\lambda)}-n\right)_{n-1}\sim-\frac1{\Gamma(1-\lambda)n^{\lambda+2}} $$ Which gives the asymptotic equivalent of the sum: $$ R_N(\lambda) = \sum_{n=N}^\infty u_n\sim -\frac1{(\lambda+1)\Gamma(1-\lambda)n^{\lambda+1}} $$ This confirms the fact that increasing $\lambda$ generally improves the convergence due to the larger power law decay. However, this holds for $\lambda\not\in\mathbb N^*$. When $\lambda\in\mathbb N^*$, the prefactor vanishes so you would expect that the leading order coefficient would be even smaller. This is the case, this time, the equivalent is: $$ u_n(\lambda) \sim\frac{(-1)^\lambda(\lambda-1)!}{4n^{\lambda+3}} $$ and for the series remainder: $$ R_N(\lambda)\sim \frac{(-1)^\lambda(\lambda-1)!}{4(\lambda+2)n^{\lambda+2}} $$ This is consistent: larger $\lambda$ leads to a faster asymptotic convergence. Furthermore, the exponent is improved by a factor $1/n$ compared to neighbouring $\lambda$.

However there is a subtle behaviour as $\lambda\to \infty$. The issue is that the previous asymptotic equivalent is not uniform in $\lambda$. For $n \ll \lambda$ which is possible due to the separation of scale, you rather recover the Leibniz formula: $$ u_n(\lambda)\sim \frac{(-1)^n}{2n-1} $$ which has a slower convergence for $1\ll N\ll\lambda$: $$ R_N \sim \frac{(-1)^N}{2N} $$ The region where this is valid grows linearly as $\lambda\to\infty$ and "contaminates" the faster power law tail. You can already predict the downfall of the latter by noticing its rapidly increasing factorial prefactor.

You can compare this to the simple formula with geometric convergence like. Take for example $\tan(\pi/6) = 1/\sqrt3$: $$ \pi = 2\sqrt3\sum_{n=0}^\infty \frac{(-1)^n}{3^n(2n+1)} $$ Obviously, this formula is superior asymptotically, but you could imagine that the new formula could have a good head start and give the first digits with fewer terms. For it to have a good head start, you need to have a relatively small $\lambda$ or else you recover the first terms of the Leibniz formula. The $n$ for which this happens is before the region of validity of the asymptotic equivalent, but you can still observe the behaviour numerically:

In short, no, compared to the most simple geometric converging formula, the formula is an improvement only for the first couple digits, and asymptotically pretty terrible.