Prove $\sum_{k=1}^{n} \frac{1}{k}\binom{n}{k}^{-1}=\sum_{k=1}^{n} \frac{1}{k}\frac{1}{2^{n-k}}$

Question

While playing around with the summation presented in a recent answer, I noticed that the following seems to be empirically true (up to $n=100$ via Mathematica):

$$\sum_{k=1}^{n} \frac{1}{k}\binom{n}{k}^{-1}=\sum_{k=1}^{n} \frac{1}{k}\frac{1}{2^{n-k}}$$

I'm not so familiar with summations involving reciprocals of binomial coefficients, and I haven't (yet) found an earlier question which covers this. Judging from earlier answers to such questions, they often revolve around the integral representation $$\binom{n}{k}^{-1}=k\int_0^1 (1-t)^{k-1}t^{n-k}dt$$ as a means to clear the summation over $k$. This initially seems attractive, particularly the role of $1/k$ to clear the coefficient. Here, though, the summation over $k$ is the entire point, so I don't see how that helps. Alternatively, we can straightforwardly pass the RHS to a generating function:

\begin{align} \sum_{n=1}^\infty \sum_{k=1}^n \frac{2^{k-n}}{k}x^n &=\sum_{k=1}^\infty \frac{2^k}{k}\sum_{n=k}^\infty \left(\frac{x}{2}\right)^n\\ &=\sum_{k=1}^\infty \frac{2^k}{k}\frac{(x/2)^k}{1-x/2}\\ &=\frac{1}{1-x/2}\sum_{k=1}^\infty \frac{x^k}{k}=\frac{\ln(1-x)}{1-x/2} \end{align}

But then it's not obvious how to relate this to $\binom{n}{k}^{-1}$.

Answer 1

We seek to show that

$$\sum_{k=1}^n \frac{1}{k} {n\choose k}^{-1} = \sum_{k=1}^n \frac{1}{k} \frac{1}{2^{n-k}}.$$

Recall from MSE 4316307 the following identity which was proved there: with $1\le k\le n$

$$\frac{1}{k} {n\choose k}^{-1} = [v^n] \log\frac{1}{1-v} (v-1)^{n-k}.$$

We get for the LHS

$$[v^n] \log\frac{1}{1-v} (v-1)^{n-1} \sum_{k=1}^n (v-1)^{-(k-1)} \\ = [v^n] \log\frac{1}{1-v} (v-1)^{n-1} \frac{1-1/(v-1)^n}{1-1/(v-1)} \\ = [v^n] \log\frac{1}{1-v} (v-1)^n \frac{1-1/(v-1)^n}{v-2}.$$

We get two pieces, the simple one is

$$-[v^n] \log\frac{1}{1-v} \frac{1}{v-2} \\ = \frac{1}{2} [v^n] \log\frac{1}{1-v} \frac{1}{1-v/2} = \frac{1}{2} \sum_{k=1}^n \frac{1}{k} \frac{1}{2^{n-k}}.$$

The second piece is

$$\;\underset{v}{\mathrm{res}}\; \frac{1}{v^{n+1}} \log\frac{1}{1-v} (v-1)^n \frac{1}{v-2}.$$

Now put $v/(v-1) = w$ so that $v=w/(w-1)$ and $dv = -1/(w-1)^2 \; dw$ to get

$$- \;\underset{w}{\mathrm{res}}\; \frac{1}{w^{n+1}} (w-1) \log\frac{1}{1-w/(w-1)} \frac{1}{w/(w-1)-2} \frac{1}{(w-1)^2} \\ = - \;\underset{w}{\mathrm{res}}\; \frac{1}{w^{n+1}} \log(1-w) \frac{1}{2-w} = \frac{1}{2} \sum_{k=1}^n \frac{1}{k} \frac{1}{2^{n-k}}.$$

Add the two pieces to obtain

$$\sum_{k=1}^n \frac{1}{k} \frac{1}{2^{n-k}}$$

as claimed.

Answer 2

Note $$\sum_{k=1}^n\frac{1}{k\binom nk}=\sum_{k=1}^n\frac{1}{n\binom{n-1}{k-1}}$$ This answer derives $$\sum_{k=0}^n \frac{1}{\binom{n}{k}} = \sum_{k=0}^n \frac{n+1}{n+1-k} \frac{1}{2^k}$$ Therefore, $$\sum_{k=1}^n\frac{1}{k\binom nk}=\frac1n\sum_{k=1}^n\frac{n}{n-k+1}\frac{1}{2^{k-1}}=\sum_{k=1}^n\frac{1}{k\,2^{n-k}}$$ Hope this helps. :)

Answer 3

Step 1. Developing from the beta function identity as pointed out by OP,

$$ \frac{1}{k\binom{n}{k}} = \int_{0}^{1} t^{k-1}(1-t)^{n-k} \, \mathrm{d}t = \int_{0}^{\infty} \frac{u^{k-1}}{(1+u)^{n+1}} \, \mathrm{d}u $$ where we applied the substitution $u = \frac{t}{1-t}$. Summing both sides for $k = 1, 2, \ldots, n$,

$$ \begin{align*} S_n := \sum_{k=1}^{n} \frac{1}{k\binom{n}{k}} &= \int_{0}^{\infty} \sum_{k=1}^{n} \frac{u^{k-1}}{(1+u)^{n+1}} \, \mathrm{d}u \\ &= \int_{0}^{\infty} \frac{1 - u^n}{(1 - u)(1+u)^{n+1}} \, \mathrm{d}u \\ &= \text{PV}\!\!\int_{0}^{\infty} \frac{1}{(1 - u)(1+u)^{n+1}} \, \mathrm{d}u - \text{PV}\!\!\int_{0}^{\infty} \frac{u^n}{(1 - u)(1+u)^{n+1}} \, \mathrm{d}u \\ &= 2 \, \text{PV}\!\!\int_{0}^{\infty} \frac{1}{(1 - u)(1+u)^{n+1}} \, \mathrm{d}u, \tag{1} \end{align*} $$ where we applied the substitution $u \mapsto \frac{1}{u}$ in the last line.

---

Step 2. Now let $f(z) = \frac{1}{(1 - z)(1+z)^{n+1}}$ be the integrand in $\text{(1)}$, and let $\operatorname{Log}(z)$ denote the complex logarithm with the branch satisfying $\operatorname{Arg}(z) \in [0, 2\pi)$. We then consider the residue computation

$$ \frac{1}{2\pi i} \int_{\mathcal{C}} f(z) \operatorname{Log}(z) \, \mathrm{d}z = \mathop{\underset{z=-1}{\text{Res}}} f(z)\operatorname{Log}(z) \tag{2} $$ along the keyhole contour $\mathcal{C}$^src)

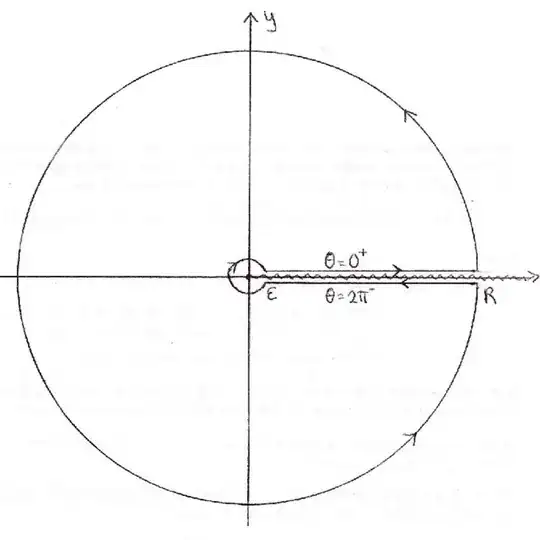
wrapping the positive $x$-axis. Letting the outer radius $R \to \infty$ and using the fact that the jump size across the branch cut satisfies

$$ {\color{blue}{\operatorname{Log}(x + 0^+i)}} - {\color{red}{\operatorname{Log}(x + 0^-i)}} = -2\pi i$$

for $x > 0$, the identity $\text{(2)}$ reduces to

$$ \begin{align*} \mathop{\underset{z=-1}{\text{Res}}} f(z)\operatorname{Log}(z) &= \frac{1}{2\pi i} \int_{0}^{\infty} f(z)[{\color{blue}{\operatorname{Log}(z + 0^+i)}} - {\color{red}{\operatorname{Log}(z + 0^-i)}}] \, \mathrm{d}z \\ &= -\text{PV}\!\!\int_{0}^{\infty} f(z) \, \mathrm{d}z - \frac{1}{2} \, \mathop{\underset{z=1}{\text{Res}}} \, (2\pi i) f(z). \end{align*} $$

(The half-residue comes from lower part of the keyhole contour in the vicinity of $z = 1$.) Hence,

$$ \begin{align*} \text{PV}\!\!\int_{0}^{\infty} f(z) \, \mathrm{d}z &= - \mathop{\underset{z=-1}{\text{Res}}} f(z)\operatorname{Log}(z) - \frac{1}{2} \mathop{\underset{z=1}{\text{Res}}} (2\pi i) f(z) \\ &= - \mathop{\underset{w=0}{\text{Res}}} \frac{i\pi + \log(1-w)}{(2 - w) w^{n+1}} - i \pi \mathop{\underset{w=0}{\text{Res}}} \frac{1}{(-w)(2+w)^{n+1}} \end{align*} $$

Since the left-hand side is real, the same is true for the right-hand side, leading to the equality

$$ \begin{align*} \text{PV}\!\!\int_{0}^{\infty} f(z) \, \mathrm{d}z &= - \mathop{\underset{w=0}{\text{Res}}} \frac{\log(1-w)}{(2 - w) w^{n+1}} = -[w^n]\frac{\log(1-w)}{(2 - w)} \\ &= [w^n]\left( \sum_{j=0}^{\infty} \frac{w^j}{2^{j+1}} \right)\left( \sum_{k=1}^{\infty} \frac{w^k}{k} \right) = \sum_{k=1}^{n} \frac{1}{k 2^{n+1-k}}. \end{align*} $$

Finally, plugging this back into $\text{(1)}$ completes the proof.