The following would probably get me booted out of a shinto monastery, but posting it anyway. Alas, I need two pictures to make it clear, but I think the configuration is more "rigid" than the one in Blue's first solution — I don't need to assume any pair of points of tangency on a circle to be diametrically opposite (unless the rest of picture forces that to be the case).
The ingredients are:
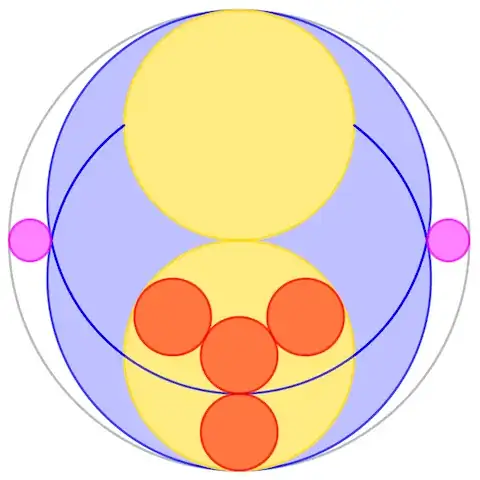
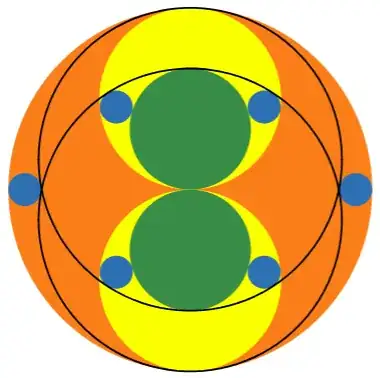
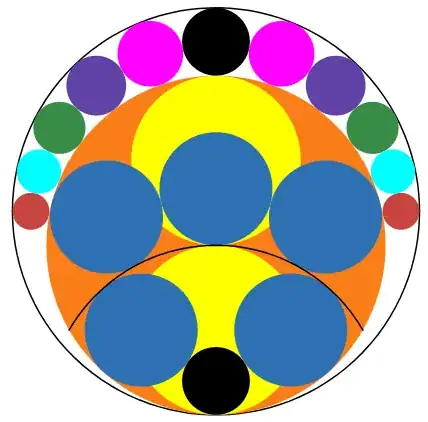
- The example Sangaku realizing the $1:7$ ratio.
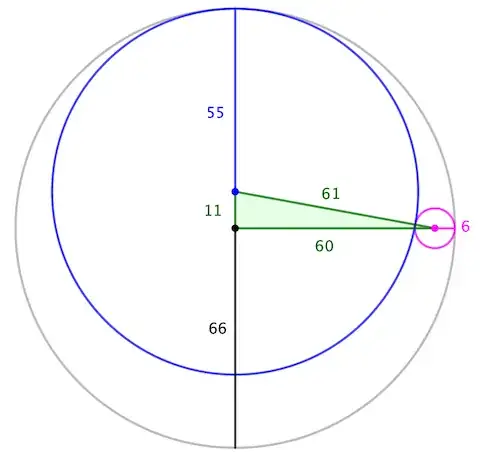
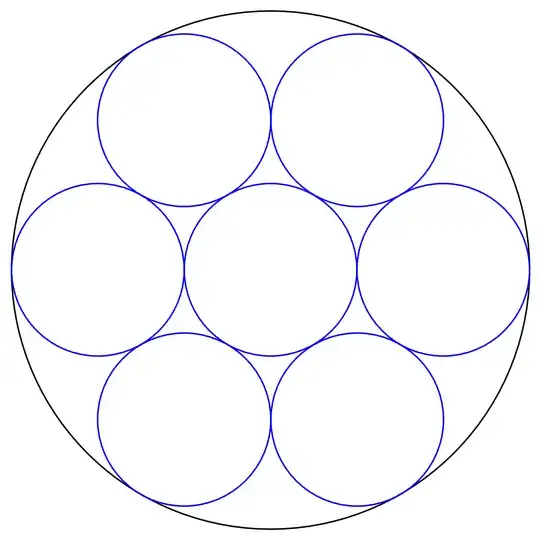
- When we have a hexagonal ($\approx$honeycomb) arrangement of seven circles of equal radii $R$ (blue in the image below), the central one tangent to the other six, forming a bracelet around the central one, then the bigger circle (black) circumscribing the whole lot necessarily has radius $3R$.
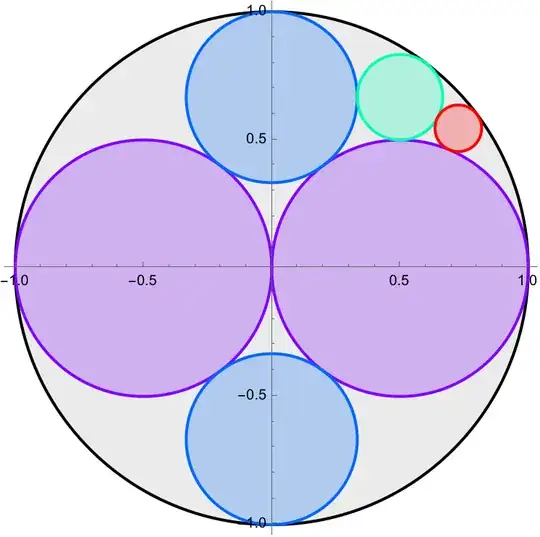
- In the following arrangement of circles of three radii $R_1$(black), $R_2$(red) and $R_3$(blue) we have the relation
$$
R_3=\frac{R_1 (R_1-R_2)}{R_1+3R_2}.\qquad(*)
$$
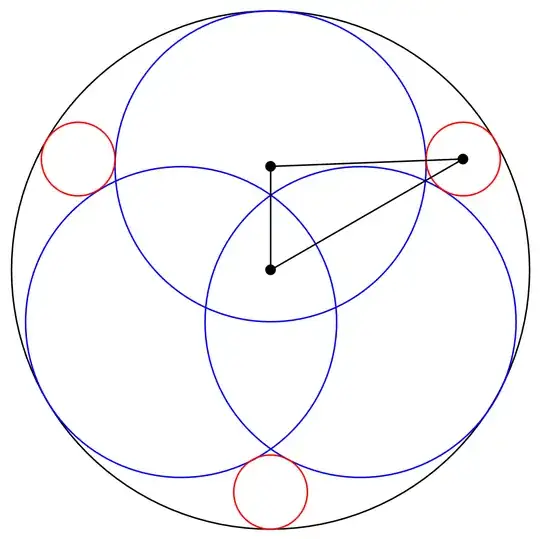
Proof. Look at the triangle with vertices at the centers of the obvious circles. Two of its sides have lengths $R_1-R_2$ and $R_1-R_3$ with the angle between equal to $\alpha=\pi/3$. The third side has length $R_2+R_3$. Apply the law of
cosines to that triangle. Plug in $\cos\alpha=1/2$, and solve for $R_3$ from the resulting equation. QED
Observe that the roles of $R_2$ and $R_3$ are interchangeable (or red vs. blue circles), and we can equally well calculate $R_2$ when knowing $R_1$ and $R_3$. In particular, when $R_2=R_1/3$ the formula ($*$) gives $R_3=R_2$ as in the hexagonal layout of the second bullet.
Observe that by selecting $R_1=1$, $R_2=1/7$ we get $R_3=3/5$. With those choices the above diagram is a key part of the given Sangaku yielding that precious $1:7$ ratio. It is still crucial that the four circles of radius $R_4=1/5$ (blue in Dan's image) fit exactly as prescribed. If you take a peek at Dan's link you will learn that those blue circles of radius $R_4$ are a part of the hexagonal picture (see my second bullet).
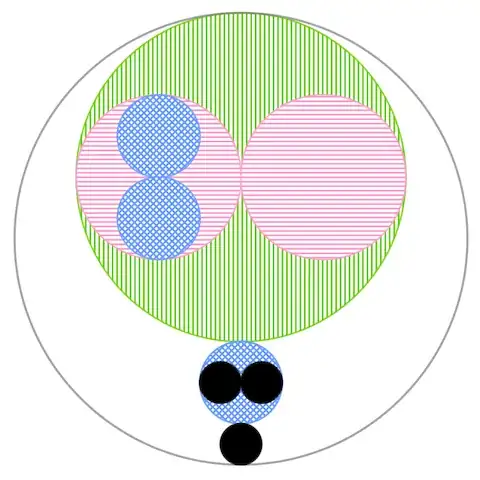
The remaining piece is that by selecting $R_1=1$, $R_2=1/11$, the formula (*) yields $R_3=5/7$. This gives us the following solution consisting of two pictures:
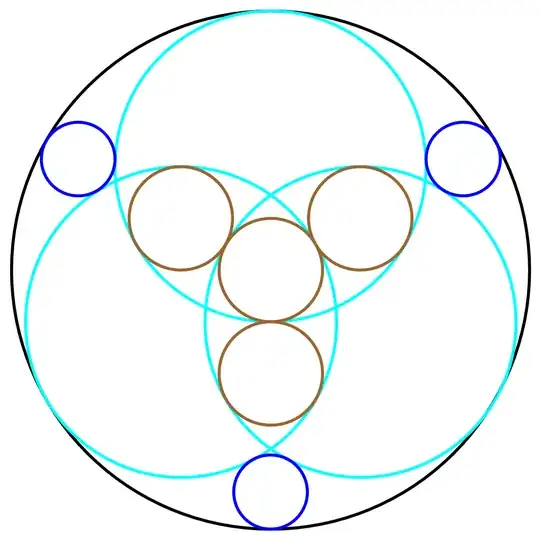

The picture on the left is essentially the $1:7$ Sangaku Dan posted. I recap the argument. Assume that the radius of the black circles is $R_{\text{black}}=1$. The four brown circles form a part of that hexagonal pattern, and this quickly leads to the relation
$$R_{\text{cyan}}=3 R_{\text{brown}}.$$
But the diameter of a cyan circle is clearly the sum of the radii of the brown and black circles, so we have
$$2R_{\text{cyan}}=R_{\text{brown}}+R_{\text{black}}.$$
From this pair of equations and the known value of $R_{\text{black}}$ we easily solve $R_{\text{brown}}=1/5$. Hence $R_{\text{cyan}}=3/5$ matching with our example use of the formula $(*)$. So the left diagram, indeed, yields $R_{\text{blue}}=1/7$.
Moving to the diagram on the right. In its center we have a hexagonal arrangement of blue circles circumscribed by the gray circle, so we have
$$
R_{\text{gray}}=3R_{\text{blue}}=3/7.
$$
But, analogously to the second step in our handling of the left diagram, the diameter of a red circle is the sum of radii of grey and black circles, so
$$
R_{\text{red}}=\frac12\left(R_{\text{grey}}+R_{\text{black}}\right)=5/7.
$$
But this matches perfectly our second example application of the formula $(*)$, and we can conclude that
$$
R_{\text{green}}=\frac1{11}.
$$