Functional equation with $f(x+y)=f(x)f(1-y)+f(1-x)f(y)$

Question

Let $f:\Bbb R\to\Bbb R$ such that

1. $f(x+y)=f(x)f(1-y)+f(1-x)f(y)$,
2. $f(x)$ is strictly increasing on $[0,1]$.

Find the solution set to $f(x)\ge\frac12$.

This is a problem form a mock test with no solution.

Here is my attempt. Let $P(x,y)$ be the assertion $f(x+y)=f(x)f(1-y)+f(1-x)f(y)$.

1. By $P(1-x,1-y)$ and $P(x,y)$,$$f(2-x-y)=f(1-x)f(y)+f(x)f(1-y)=f(x+y),$$and so $f(t)=f(2-t)$.
2. By $P(0,0)$ and $P(1,0)$, $\left\{\begin{smallmatrix}f(1)=f^2(1)+f^2(0),\\f(0)=2f(0)f(1)\\f(0)<f(1)\end{smallmatrix}\right.$, so $f(0)=0$, $f(1)=1$ or $f(0)=-\frac12$, $f(1)=\frac12$.

I tried plugging many other values, but more and more cases arose. Many we should eliminate on case produced above immediately.

Answer 1

$P(x,y)$ is denoted as the writer. And now we have $f(x) = f(2 - x)$.

If $f(0) = -\frac12$ $f(1) = \frac12$:

By $P(x,1)$, $f(x + 1) = \frac12 f(1-x) - \frac12 f(x)$. Combined with $f(x + 1) = f(2 - (x + 1)) = f(1-x)$, we have $f(x)=-f(1-x)=-f(x+1)$. Hence $f(x)=f(x+2)$.

By $P(\frac12,-\frac12)$, $-\frac12=f(\frac12)f(\frac32)+f(\frac12)f(-\frac12)=2f(\frac12)^2$, a contradiction.

Thus $f(0)=0$, $f(1)=1$.

$0=f(2)=f(2-y)f(1-y)+f(-1+y)f(y)$, so$f(1-y)=-f(-1+y)$ for $f(y) \ne 0$.

By $P(x,-1)$, $f(x-1)=f(-1)f(1-x)$. Let $f(x-1) \ne 0$, then $f(-1) = -f(1) = -1$, and $f(x)=-f(-x)$. $f(x) = -f(-x) = -f(2+x) = f(x+4)$

By $P(\frac13,\frac13)$, $f(\frac23)=2f(\frac13)f(\frac23) \implies f(\frac13) = \frac12$. Then $[\frac13+4k,2-\frac13+4k] \text{(k is an integer)}$ are the all sets.

Answer 2

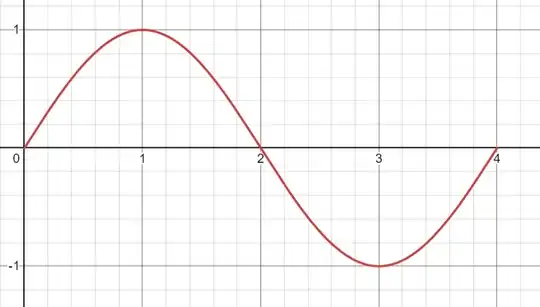
I want to add the following result that maybe can be interesting:

$\textbf{Theorem.}$ If the function satisfy our condition and it is derivable at the points $0$ and $1$, then

$$f(x)=\sin\left(\left(\frac{\pi}{2}+2\pi k\right)x\right), \qquad k\in \mathbb Z.$$

$\textit{Remark.}$ First of all we observe that we have three important equations

$$f(1)=f(x+(1-x))=f^2(x)+f^2(1-x), \qquad f(2x)=f(x+x)=2f(x)f(1-x)$$

and then

$$f(1)+f(2x)=\left(f(x)+f(1-x)\right)^2.$$

$\textbf{Lemma.}$ $f(0)=0$, and $f(1)=1$.

$$f(1)=f(x+(1-x))=f^2(x)+f^2(1-x), \qquad and \qquad f(2x)=f(x+x)=2f(x)f(1-x)$$

The first equation tells us $f(1)\neq 0$ otherwise f is constantly zero.

Morevoer, we use them to say

$$f(1)=f^2(1)+f^2(0), \qquad f(0)=2f(0)f(1) \implies f(1)+f(0)=(f(1)+f(0))^2$$

This means $f(1)+f(0)$ can be only $0$ or $1$.

By contradiction, if $f(1)+f(0)=0$, then we would have $f(1)=2f(1)^2$, which implies $f(1)=\frac{1}{2}$, and $f^2(0)=\frac{1}{4}$, so $f(0)=-\frac{1}{2}$.

However, $f(1)=2f^2(\frac{1}{2})$, that implies $f(\frac{1}{2})= \pm\frac{ 1}{2}$, that contradicts the fact $f$ is increasing in $[0,1]$.

This forces $f(1)+f(0)=1$. By contradiction, if $f(0)\neq 0$, then we would have $f(1)=f(0)=\frac{1}{2}$, which is still not possibile.

Therefore, $f(0)=0$, and $f(1)=1$.

$\textbf{Lemma 2.}$ If $f$ is derivable at $0$ and $1$, then it is derivable everywhere, and it satisfies the Cauchy problem $$ \begin{cases} f'(x)=f(1-x)f'(0) \\ f(0)=0, f(1)=1 \end{cases}$$

$\textit{Proof.}$ It is sufficient to observe that

$$ \frac{f(x+h)-f(x)}{h}=\frac{f(x)f(1-h)-f(x)+f(1-x)f(h)}{h}=f(x)\frac{f(1-h)-1}{h}+f(1-x)\frac{f(h)}{h}. $$

Since $f(0)=0$ and $f(1)=1$, then when $h\to 0$ we obtain

$$\lim_{h\to 0}\frac{f(1-h)-1}{h}=-f'(1), \qquad \lim_{h\to 0}\frac{f(h)}{h}=f'(0).$$

Thus the derivative of $f$ at $x$ exists and it is equal to

$$f'(x)=-f(x)f'(1)+f(1-x)f'(0).$$

We observe that $f'(1)=-f'(1)+0$ so that $f'(1)=0$ and we obtain the thesis.

$\textbf{Lemma 3.}$ The function $f$ satisfies the Cauchy problem $$ \begin{cases} f''(x)=-(f'(0))^2f(x) \\ f(0)=0, f(1)=1 \end{cases}$$

$\textit{Proof.}$ $D(f'(x))=D(f(1-x)f'(0))=-f'(1-x)f'(0)=-f(x)(f'(0))^2.$

Now we can prove the theorem:

$\textit{Proof of the theorem.}$It is easy to see that the solution of the ODE $f''(x)=-k^2f(x)$ is

$$f(x)=a\cos(kx)+b\sin(kx).$$

In our case we have

$$f(0)=0=a, \qquad f(1)=1=b \sin(k).$$

However, $k=f'(0)=bk\cos(kx)_{x=0}$, so that $b=1$ and $sin(k)=1$ implies $k=\frac{\pi}{2}+2t\pi$, $t\in\mathbb Z$ and finally

$$ f(x)=\sin\left(\left(\frac{\pi}{2}+2\pi t\right)x\right).$$

I don't actually know what happens if we do not suppose that $f$ is derivable at $0$ and $1$. If someone want to help me to find a solution, it would be nice :).

Answer 3

$P(x,y) \implies f(x+y)=f(x)f(1-y)+f(1-x)f(y)$

As you noted we have two possibilities: $f(0)=0$ and $f(1)=1$ or $f(0)=-\frac12$ and $f(1)=\frac12$.

We also note the first relation you found: $f(x)=f(2-x)\tag {1}$

---

First possibility is $f(0)=-\frac 12$ and $f(1)=\frac 12$.

Consider $P\left(\frac 12, \frac 12\right)\implies f(1)=2f^2(1/2)\implies f(1/2) = \pm \frac 12$, contradicting the increasing nature of $f$ on $[0,1]$.

---

The other possibility is $f(0)=0$ and $f(1)=1$.

Note we have $P(2,-x) \implies f(2)f(1+x) + f(-x)f(-1) = f(2-x) = f(x)$ ie $$f(x) = f(-x)f(-1)\tag{2}$$ Setting $P(2,-1)$ gives $f(1) = f(-1)f(-1)$ as $P(2,-1)\implies f(1)=f(2)f(2)+f(-1)f(-1)=f^2(-1)$. Thus $f(-1)=\pm 1$.

Also notice that $P(1/3, 1/3) \implies f(2/3) = 2f(1/3)f(2/3)$ so that $f(1/3) = \frac12\tag3$ since $f(2/3) \neq 0$.

Then we divide into cases:

Case $1$: $f(-1)=1$ and thus when $f(-x)=f(x)$ (by $(2)$).

But then $P(1/2, -1/2) \implies f(0) = f(1/2)f(3/2) + f(-1/2)f(1/2) \implies f(1/2)f(3/2)=-f(-1/2)f(1/2)\implies f(1/2)f(3/2)=-f(1/2)f(1/2)$, contradiction since one side is positive and the other negative. No solution here hence.

Case $2$: $f(-1) = -1$ ie $f(x) = -f(-x)$ by $(2)$ meaning $f$ is odd.

So $f(x+4) = f(x)f(-3)+f(4)f(1-x) = -f(x)f(3) = -f(x)f(-1) = f(x)$. Then $f$ is periodic $\bmod 4$. Using $(1)$ and the odd nature of $f$, one can roughly sketch out the values of $f$, as given below:

Then the solutions in $[0,4]$ are $\left[\frac13, \frac53\right]$ by $(3)$ and so the solutions generally are $\left[\frac13 + 4n, \frac53 + 4n\right]$ where $n\in \mathbb Z$.

Answer 4

Working in steps:

1. Use $P(0,0)$ and $P(\frac{1}{2}, \frac{1}{2})$ to show $f(0)=0$ and $f(1) = 1$

2. Use $P(x, x)$ to find an $x\in[0, 1]$ such that $f(x) = \frac{1}{2}$

3. Use $P(1,x)$ to extend the result to all of $\mathbb{R}$

Can you fill in the gaps?

Answer 5

I thought it would be worthwhile to add the general solution to the functional equation, without any further assumptions.

Firstly we handle the case where $f(0) \ne 0$. In this case then

$$f(x) = f(x)f(1) + f(1-x)f(0)$$ so $$f(1-x) = Cf(x) \, \textrm{where }C = \frac{1-f(1)}{f(0)} $$

But then we get that

$$f(x+y) = 2Cf(x)f(y)$$

In the case where $C=0$ we hence know that $f(x) = 0$ Otherwise $f(x) = E(x)/2C$ where $E$ a solution to the exponential equation $E(x+y) = E(x)E(y)$. This is a well-studied equation, see e.g. Overview of basic facts about Cauchy functional equation

Subbing this into the defining equation will give us that the only possibility is $f(x) = \frac 12$ or $f(x) = 0$.

Now we handle the more interesting case where $f(0) = 0$ and $f \ne 0$

Firstly we get some basic parity results as well as some specific values.

We sub $y=0$ to get

$$f(x)= f(1)f(x)$$

Hence $f(1) = 1$

Furthermore we can sub $y=1$

$$f(x+1) = f(1-x) $$

Then

$$\begin{align}f(x) &= f(1 + (x-1))\\ &= f(x-1)f(0) + f(2-x)f(1)\\ &= f(2-x)\\ &=f(2)f(1+x) + f(-1)f(-x)\\ &= f(1+1)f(1+x) + f(-1)f(-x)\\ &= f(1-1)f(1+x) + f(-1)f(-x)\\ &= f(-1)f(-x)\end{align}$$

Subbing in $x=1$ tells us the $|f(-1)| = 1$. So we have that $f$ is odd or even. If f is even.

$$\begin{align}f\left ( \frac x2 + \frac x2 \right ) &= f \left (\frac x2\right )f \left (1- \frac x2 \right ) + f \left ( \frac x2 \right )f\left (1- \frac x2\right ) \\ &= f \left (\frac x2\right )f \left (1- \frac x2 \right ) + f \left ( -\frac x2 \right )f\left (1+ \frac x2\right )\\ &= f \left (\frac x2 - \frac x 2\right )\\ &= 0 \end{align} $$

Now we look at the case where $f$ is odd.

Let $g(x) = f(1-x) + if(x)$

Then

$$\begin{align} g(x+y) &= f(1-x-y)+ if(x+y)\\ &= f(1-x)f(1-y) + f(x)f(-y) + i(f(x)f(1-y) + f(1-x)f(y)\\ &= f(1-x)f(1-y) - f(x)f(y) + i(f(x)f(1-y) + f(1-x)f(y)\\ &= (f(1-x) + if(x) ) ( f(1-y) + if(y) ) \\ &= g(x)g(y) \end{align} $$

Furthermore $g(1) = i$ and by parity arguments $$f(x) = \frac{g(x) - g(-x)}{2i}$$

Now note that for since $f$ is real-valued. We have (using $(\cdot )^*$ to denote the complex conjugate.)

$$\begin{align} \frac {g(x) - g(-x)}{2i} &= \frac{g(x)^* - g(-x)^*}{-2i}\\ -ig(x) +\frac i {g(x)} &=ig(x)^* -\frac i {g(x)^*} \\ \frac 1 {g(x)^*}+\frac 1 {g(x)} &=g(x)^*+ g(x) \\ \frac {g(x)^*+ g(x) }{g(x)g(x)^*} &=g(x)^*+ g(x) \\ \end{align} $$

So either $g(x)$ is purely imaginary or $|g(x)| = 1$. In the case where $g(x) \ne 1$ and $g(x)$ is purely imaginary then $g(2x)$ is real and $|g(2x)| \ne 1$. Hence $|g(x)|= 1$ for all $x$.

To summarise what we have so far. Either $f$ is one of the constant solutions $x \to 0$ or $x \to \frac 12$. Otherwise there is a function such that

• $g: \mathbb R \to \mathbb C$
• $g(x+y) = g(x)g(y)$
• $|g(x)| = 1$
• $g(1) = i$
• $f(x) = \frac{g(x) - g(-x)}{2i}$

It's easy to verify that an $f$ constructed like this is a solution.

To construct a $g$ satisfying these conditions. Let $\mathfrak B$ be a hamel basis of $\mathbb R$ over $\mathbb Q$ containing 1. Furthermore pick some $k \in \mathbb Z $ Then for $b \in \mathfrak B$ pick real numbers $a_b$ with $a_1 = \frac \pi 2 + 2k \pi $

$$ g \left ( \sum_{b \in \mathfrak B} q_b b \right ) = \exp \left ( i \left ( \sum_{b \in \mathfrak B} q_b a_b\right )\right ) $$

It's easy to verify that this is the general $g$ satisfying the conditions.