I'm trying to get the four concepts listed in the title straight in my mind and elucidate the relationship between them. Could someone check the following statements and let me know if they are all correct?
- In a domain, prime elements are irreducible.
- In a UFD, irreducible elements are prime.
- Prime elements generate prime ideals.
- In a PID, each nonzero prime ideal is generated by a prime element which is unique up to a unit.
- In a PID, irreducible elements generate maximal ideals.
- In a PID, each maximal ideal is generated by an irreducible element which is unique up to a unit.
- R/I is a domain iff I is a prime ideal in R. Therefore, all maximal ideals are prime.
- In a PID, all nonzero prime ideals are maximal.
This is summarized in the following diagram.
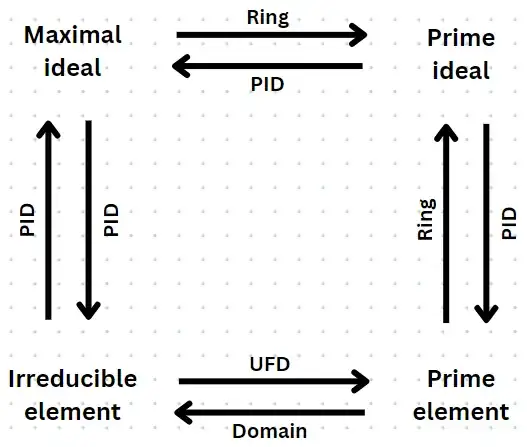 By the time we reach a PID, the concepts are essentially interchangeable.
By the time we reach a PID, the concepts are essentially interchangeable.