Minimum number of dominoes needed in order to force a tiling of a 2n by 2n board

Question

I have found a problem from the Peruvian Math Olympiad (ONEM 2012) and have been working on it for a couple hours but the solution seems to evade me. The problem is so: (translated via google translate)

A domino is a 1x2 or 2x1 rectangle. Diego wants to completely cover a 6x6 board using 18 dominoes. Determine the smallest positive integer k for which Diego can place k dominoes on the board (without overlapping) such that the remainder of the board can be covered uniquely using the remaining dominoes.

I am quite sure that the answer is 3, but I have been unable to prove it. I know that k is less than or equal to 3, as if one places 3 dominoes in a zigzag, the rest of the board becomes forced, but I can't seem to prove that k > 2. I've tried a simpler case with a 4 by 4 board, and have found that k is exactly equal to 2 in this case with a proof like so:

It is clear that there are 2 ways to tile a 2 by 2 board with 2 dominoes. Next, we shall prove that k for a 4 by 4 board is greater than 1. Say for the sake of contradiction that k is equal to 1. Let us first consider the case where the domino is completely contained in the center 2 by 2 square of the full 4 by 4 board. Then, we can complete the inner 2 by 2 square and we immediately see that there are 2 ways to tile the board, one with two horizontal tiles on the top row, and one with one horizontal tile on the top row. Therefore, we can consider the case where the placed domino does not intersect with the center 2 by 2 square. Then again we see that there are two tilings for the 4 by 4 board, as while the perimeter of the board is determined, the center 2 by 2 square can be tiled in two different ways. Finally, we consider the case where the placed domino intersects the center 2 by 2 square, but is not fully contained in it. Then, we see that we can split the board into 4 2 by 2 quadrants, and that the only determined quadrant is the quadrant that contains the placed domino. Therefore, there must be at least 8 different tilings for the rest of the board, since each of the 3 non determined quadrants can be tiled 2 different ways. With this, we have a contradiction and we see that k must be greater than 1 for a 4 by 4 board. We can then prove that k = 2 by checking that if we place the two dominoes in a tetris piece in the corner, the rest of the board is determined.

Here are the drawings that represent the way to force the rest of the tiling for both the 6 by 6 case and the 4 by 4 case: 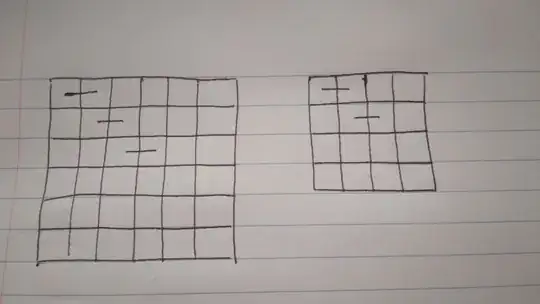The short lines that go between two squares represent which two squares the particular domino would take place.

I've tried to extend my argument from the 4 by 4 case to the 6 by 6 case, but the argument seems like it would require a ton of casework and feels wrong somehow. I've searched online for the official solution to this problem, but I can't seem to find it. Is there a better way to show that k = 3 for a 6 by 6 board?

Answer 1

Here's a solution which reduces the casework for the $6 \times 6$ board, but I don't think it will scale to larger boards.

We say that a board with some given dominoes on it is tileable if we can place dominoes on the rest of the board filling it. We say it is mulitply tileable if we can do this in at least two different ways.

Observe that a $2 \times 6$ board with one given domino is multiply tileable, and a $1 \times 6$ board is tileable.

We call two given dominoes horizontally (vertically) separable if no horizontal row (vertical column) contains part of both dominoes. Observe that any two dominoes are horizontally or vertically separable. Without loss of generality, suppose our two given dominoes on the $6 \times 6$ board are horizontally separable.

If we are able to partition the rows of the $6 \times 6$ board such that our two given dominoes are in separate $2 \times 6$ parts, we are done. In fact, we are done unless one domino is contained in the top row, one position away from the left (WLOG), and the second domino intersects the second row. If we are able to partition the columns of the $6 \times 6$ board such that our two given dominoes are in separate $2 \times 6$ parts, we are done as before. Thus there are are only six cases for the second domino, two of which lead to blocking off a corner and are hence not tileable, and the others are easy to show are multiply tileable.

Answer 2

Let's rephrase the problem using the $2k \times 2k$ grid graph $G_k = (V_k, E_k)$. A domino tiling corresponds to a perfect matching of the graph. The problem is to find a partial matching of the graph such that a unique perfect matching is forced.

Suppose we have a matching $M$ and a cycle $C$ in a graph $G = (V, E)$. Define that the cycle $C$ is alternating for $M$ if the cycle alternates between edges in $M$ and $E \setminus M$.

Lemma: For a graph $G$ and a perfect matching $M$, there is no alternating cycle for $M$ if and only if $M$ is the unique perfect matching.

• $\impliedby$ If there is an alternating cycle $C$ for $M$, then we can construct a different perfect matching of $G$ by taking the symmetric difference $M \Delta C$.
• $\implies$ Suppose there are two different perfect matchings $M_1, M_2$. Then, the symmetric difference $D := M_1 \Delta M_2$ consists of a disjoint union of cycles because the degree of each vertex restricted to $D$ will be $1 \pm 1$. Then we can take any cycle.

Therefore, the original question is reduced to constructing a perfect matching $M$ such that $k$ disjoint alternating cycles for $M$ exists. Because each edge can only block one alternating cycle, we can conclude that at least $k$ dominoes must be used in the original problem.

We inductively construct a perfect matching $M_k$ for the $2k \times 2k$ grid graph $G_k$ and a set of alternating cycles $C_k$ for $M_k$. This is the same construction as the one shown in the OP image:

• $M_0$ and $C_0$ are empty.
• To construct $M_{k+1}$, we first place $M_k$ in the center. Then, we add alternating edges on the border of the grid, starting from $\{(1, 1), (2, 1)\}$. Let $C$ be the cycle of all border edges then it is an alternating cycle for $M_{k+1}$. Let $C_{k+1} = C_k \cup \{ C \}$.