Sangaku problem about three chords in a circle

Question

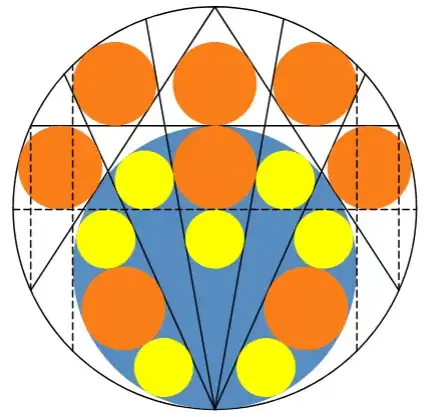
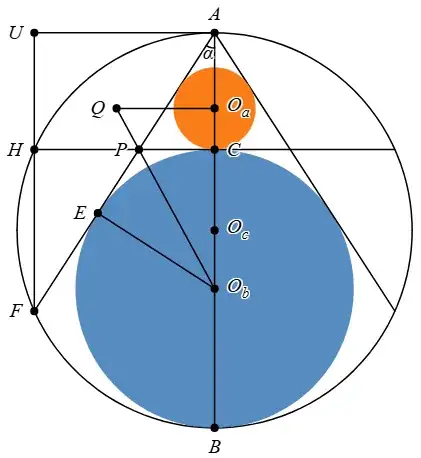
Inside circle $O$ (shown with white interior), a blue circle sits at the bottom. $O$ has two chords that meet at the top of $O$ and are tangent to the blue circle. $O$ also has a horizontal chord tangent to the blue circle. Three orange circles of equal radii are inscribed in the three regions above the horizontal chord.

Show that the diameter of the blue circle equals the width of the row of orange circles (including the gaps).

I only have computer-assisted solution. I am looking for a computer-free solution.

My computer-assisted solution

I assumed $O$ is a unit circle. Using desmos, I approximated the radii of the blue and orange circles by manually adjusting their values to get a good fit, then put those approximations into Wolfram, which suggested the following:

• The radius of blue circle, $R$, satisfies $R^3-4R^2+8R-4=0$. ($R\approx0.70440$)
• The radius of the orange circles $S$, is $R-R^2$.

I put the exact values of $R$ and $S$ into my desmos graph, and the circles and chords fit together perfectly, and indeed the width of the blue circle seems to equal the width of the row of orange circles.

Context

I was trying to prove a theorem presented by @Blue in their answer to a Sangaku question of mine, and I stumbled upon this neat result.

Fun facts

The endpoints of the horizontal chord lie directly above endpoints of the slanted chords, as noticed by @Blue in the comments.

If we add four chords that meet at the bottom of $O$ and are tangent to the left and right orange circles in the top row, then we get a total of eight congruent orange circles, and seven congruent yellow circles, and a horizontal line tangent to three orange and five yellow circles, as shown.

Answer 1

If OP’s statement holds, then there exists a unique angle $\measuredangle BAF$ (see the diagram), which does not depend on the radii of the given Sangaku configuration. For brevity, we denote this particular angle by $\alpha$. Our attempt is to find $\alpha$.

Note that the line segments $AF$ and $HC$ are externally tangent to the two $\color{red}{\text{red circles}}$ and the $\color{blue}{\text{blue circle}}$, the radii of which are $r_a$ and $r_b$ respectively. Vertical line segment $UV$ is externally tangent to the leftmost red circle and the blue circle at $S$ and $T$ respectively. The radius of the black circumscribing circle is $r_a$. This circle is internally tangent to the leftmost red circle and the blue circle at $M$ and $B$ respectively.

Two triangles $ADO_a$ and $AEO_b$ are right-angled. $${\large{\pmb{\therefore}}}\quad O_aA=\dfrac{r_a}{\sin\left(\alpha\right)}\quad\text{and}\quad O_bA=\dfrac{r_b}{\sin\left(\alpha\right)}.$$

We know that, $O_bA=O_aA+O_aC+O_bC$. Therefore, we can express $r_a$ in terms of $r_b$ and $\alpha$ as shown below. $$O_bA=\dfrac{r_b}{\sin\left(\alpha\right)}=\dfrac{r_a}{\sin\left(\alpha\right)}+r_a+r_b\quad \longrightarrow\quad r_a=\dfrac{1-\sin\left(\alpha\right)}{1+\sin\left(\alpha\right)}r_b\tag{1} $$

Similarly, since we know that, $AB=O_bA+O_bB$, we can express $r_c$ in terms of $r_b$ and $\alpha$. $$2r_c=AB=\dfrac{r_b}{\sin\left(\alpha\right)}+r_b\quad \longrightarrow\quad r_b=\dfrac{2\sin\left(\alpha\right)}{1+\sin\left(\alpha\right)}r_c \tag{2}$$

While deducing (1) and (2), we only considered spatial data of blue circle, middle red circle, and chord $AF$ with respect to black circle. To incorporate constrains imposed on the leftmost red circle by black circle and semi-chord $HC$, we need to derive the following equation.

Applying Pythagoras theorem to the right-angled triangle $O_cO_aO’_a$, we can write, $$ (O'_aO_c)^2=(O_aO_c)^2+(O'_aO_a)^2\quad\longrightarrow\quad (r_c-r_a)^2=(2r_b-r_c+r_a)^2+(r_b-r_a)^2.$$

Assuming $r_b\neq 0$, this can be simplified to get, $$ r_c=\dfrac{(r_b+r_a)^2}{4r_b}+r_b .\tag{3}$$

Now, we are in a position to check whether there exists a unique $\alpha$. To do this, substitute (1) and (2) in (3). $$ 4\dfrac{1+\sin(\alpha)}{2\sin(\alpha)}r_b^2=\left(r_b+\dfrac{1-\sin(\alpha)}{1+\sin(\alpha)}r_b\right)^2+4r_b^2$$

It is obvious that $r_b$ can be eliminated from the above equation, because $r_b\neq 0$. Further simplification yields the following cubic equation. $$ \sin^3(\alpha)+\sin^2(\alpha)+ \sin(\alpha) =1\tag{4}$$

It can be shown that the discriminant of the reduced form of (4) is greater than zero, which indicates that (4) has only one real root. With that we have proven that the Sangaku configuration described in OP’s problem statement is possible. To find the exact value of $\sin(\alpha)$, we can use Cardano’s method and Vieta’s formula. $$\sin(\alpha)=\sqrt[3]{\dfrac{17}{27}+\sqrt{\left(\dfrac{17}{27}\right)^2+\left(\dfrac{2}{9}\right)^3}}+\sqrt[3]{\dfrac{17}{27}-\sqrt{\left(\dfrac{17}{27}\right)^2+\left(\dfrac{2}{9}\right)^3}}-\dfrac{1}{3}$$ $$=\dfrac{1}{3}\left(\sqrt[3]{17+\sqrt{297}} +\sqrt[3]{17-\sqrt{297}}-1\right).\qquad\qquad\qquad\qquad$$

With this we have $\enspace\alpha=32.935120800772722797935101378469^o$.

We substitute this value in (1) and (2) to express $r_b$ and $r_a$ in terms of $r_c$. $$r_b=0.70440225747791522901900340714848\times r_c,\quad\text{and}$$ $$r_a=0.20821971713793204783928464924803\times r_c\qquad\quad$$

Answer 2

Here is a solution from a colleague of mine.

---

General strategy

Instead of assuming that the three orange circles are congruent, I assume that the endpoints of the horizontal chord lie directly above endpoints of the slanted chords (and that three orange circles are inscribed in the three regions above the horizonal chord). Then I will show that this implies, birectionally, both (1) the orange circles are congruent, and (2) the width of the row of orange circles equals the diameter of the blue circle.

---

Definitions

Assume that the largest circle is a unit circle.

Let the radii of the middle orange circle and blue circle be $r_a$ and $r_b$, respectively.

Define points:

• Points $O_a,O_b,O_c$ are the centres of the middle orange circle, blue circle, and unit circle, respectively.
• Point $P$ is the intersection of the horizontal chord and the left slanted chord.
• Point $Q$ is the intersection of $O_bP$ extended and the horizontal line through $O_a$.
• Other points are shown in the diagram below.

Let $\alpha=\angle FAB$. Let $\boxed{s=\sin\alpha}$ and $\boxed{c=\cos\alpha}$.

---

Establishing some results to be used

First I will show that $\boxed{r_b=c^2}$ and $\boxed{s^3+s^2+s=1}$.

$\begin{align} UF&=UH+HF\\ &=AC+2CO_c\\ &=(2-2r_b)+2(2r_b-1)\\ &=2r_b\\ \end{align}$

$r_b=\frac12UF=\frac12AFc=\frac12(2c)c=\color{red}{c^2}$

$r_b=AO_bs=(2-r_b)s\implies r_b=\color{blue}{\frac{2s}{1+s}}$

$\therefore \color{red}{c^2}=\color{blue}{\frac{2s}{1+s}}\implies s^3+s^2+s=1$

Now I will show that $\boxed{s=\tan\left(45^\circ-\frac{\alpha}{2}\right)}$.

$s^3+s^2+s=1$
$s^4+s^3+s^2=s$
$-s+s^4+s^3+s^2=0$
$-s+s^4+s^3+s^2+(s^3+s^2+s)=0+(1)$
$(s^2+s)^2=1-s^2$
$s^2+s=c$
$s=\frac{c}{1+s}=\frac{\cos^2\left(\frac{\alpha}{2}\right)-\sin^2\left(\frac{\alpha}{2}\right)}{1+2\cos\left(\frac{\alpha}{2}\right)\sin\left(\frac{\alpha}{2}\right)}=\frac{1-\tan^2\left(\frac{\alpha}{2}\right)}{\sec^2\left(\frac{\alpha}{2}\right)+2\tan\left(\frac{\alpha}{2}\right)}=\frac{1-\tan^2\left(\frac{\alpha}{2}\right)}{\left(1+\tan\left(\frac{\alpha}{2}\right)\right)^2}=\frac{1-\tan\left(\frac{\alpha}{2}\right)}{1+\tan\left(\frac{\alpha}{2}\right)}=\tan\left(45^\circ-\frac{\alpha}{2}\right)$

Now I will show that $\boxed{r_a=r_bs^2}$.

$\begin{align} r_a&=PC\tan\angle O_aPC\\ &=PC\tan\angle PO_bC\\ &=PC\tan\left(45^\circ-\frac{\alpha}{2}\right)\\ &=PCs\text{ using $s=\tan\left(45^\circ-\frac{\alpha}{2}\right)$}\\ &=CO_b(\tan\angle PO_bC)s\\ &=r_b\tan\left(45^\circ-\frac{\alpha}{2}\right)s\\ &=r_bs^2\\ \end{align}$

---

Showing that the orange circles are congruent

$\begin{align} O_aO_c&=1-AO_a\\ &=1-\frac{r_a}{s}\\ &=1-r_bs\text{ using $\boxed{r_a=r_bs^2}$}\\ &=1-c^2s\text{ using $\boxed{r_b=c^2}$}\\ \end{align}$

$\begin{align} QO_a&=O_aO_b\tan\left(45^\circ-\frac{\alpha}{2}\right)\\ &=(r_a+r_b)s\text{ using $\boxed{s=\tan\left(45^\circ-\frac{\alpha}{2}\right)}$}\\ &=(r_bs^2+r_b)s\text{ using $\boxed{r_a=r_bs^2}$}\\ &=r_b(s^3+s)\\ &=r_b(1-s^2)\text{ using $\boxed{s^3+s^2+s=1}$}\\ &=c^4\text{ using $\boxed{r_b=c^2}$}\\ \end{align}$

Using basic trigonometric identities, it can be shown that

$$s^3+s^2+s=1\iff (1-c^2s^2)^2=(1-c^2s)^2+(c^4)^2$$

• I showed that the left side equation is true.
• The right side equation is $(1-c^2s^2)^2={O_aO_c}^2+{QO_a}^2$.
• Pythagoras tells us that $\space{QO_c}^2={O_aO_c}^2+{QO_a}^2$.

$\begin{align} \therefore QO_c&=1-c^2s^2\\ &=1-r_bs^2\text{ using $\boxed{r_b=c^2}$}\\ &=1-r_a\text{ using $\boxed{r_a=r_bs^2}$}\\ \end{align}$

$\therefore QO_c+r_a=1$.

This means that the left orange circle's centre is at the point $Q$, which means that the left orange circle is congruent to the middle orange circle. Then by symmetry, all three orange circles are congruent.

---

Showing that the width of the row of orange circles equals the diameter of the blue circle

$\begin{align} r_a+QO_a&=r_bs^2+O_aO_b\tan\angle QO_bO_a\text{ using $\boxed{r_a=r_bs^2}$}\\ &=r_bs^2+(r_a+r_b)\tan\left(45^\circ-\frac{\alpha}{2}\right)\\ &=r_bs^2+(PC\tan\angle O_aPC+r_b)s\text{ using $\boxed{s=\tan\left(45^\circ-\frac{\alpha}{2}\right)}$}\\ &=r_bs^2+(CO_b\tan^2\angle PO_bC+r_b)s\\ &=r_bs^2+r_b(s^3+s)\text{ using $\boxed{s=\tan\left(45^\circ-\frac{\alpha}{2}\right)}$}\\ &=r_b\text{ using $\boxed{s^3+s^2+s=1}$}\\ \end{align}$

This means that the width of the row of orange circles equals the diameter of the blue circle.

Answer 3

Follows a way to obtain a solution using tangency properties. If a circle defined as $(x-x_0)^2+(y-y_0)^2=r_0^2$ is tangent to a line $y = y_1 + m(x-x_1)$ and the line is not vertical, substituting $y$ in both we obtain a polynomial in $x$:

$$ p_0(x) = x_0^2+(m x_1+y_0-y_1)^2-r_0^2-2(x_0+m(m x_1+y_0-y_1))x+(1+m^2)x^2=k_0(x-x_{t_0})^2,\ \ \ \ \forall x $$

which is equivalent to the conditions

$$ \cases{ x_0^2-k_0 x_{t_0}^2-(m x_1+y_0-y_1)^2-r_0^2=0\\ x_0-k_0 x_{t_0} + m(m x_1+y_0-y_1) = 0\\ 1+m^2-k_0^2 = 0 } $$

Analogously, if two circles $\{(x-x_0)^2+(y-y_0)^2=r_0^2, (x-x_2)^2+(y-y_2)^2=r_2^2\}$ are tangent, we have after substituting the common $y$, a polynomial in $x$:

$$ p_2(x) = k_2(x-x_{t_2})^2,\ \ \ \forall x $$

which gives the equivalent relations

$$ \cases{ r_0^4 + r_2^4 + k2 x_{t_2}^2 + 2 r_2^2 (x_0^2 - x_2^2 - (y_0 - y_2)^2) + ((x_0 - x_2)^2 + (y_0 - y_2)^2) ((x_0 + x_2)^2 + (y_0 - y_2)^2) - 2 r_0^2 (r_2^2 + x_0^2 - x_2^2 + y_0^2 - 2 y_0 y_2 + y_2^2) = 0\\ 4 r_0^2 (x_0 - x_2) + 4 r_2^2 (x_2-x_0) - 2 k_2 x_{t_2} - 4 (x_0 + x_2) ((x_0 - x_2)^2 + (y_0 - y_2)^2)= 0\\ k_2 + 4 ((x_0 - x_2)^2 + (y_0 - y_2)^2) = 0 } $$

note that $\{x_{t_0},x_{t_2}\}$ represent the double tangent points in each case. So to solve this problem, we equate four circles $\mathscr{C}_i$ and a line $\mathscr{L}$, constructing the equivalent polynomials and solving for the conditions. This gave us $12$ conditions and $12$ unknowns. Follows the MATHEMATICA script which solves it.

Clear[p, r1, r2, r3, x1, x2, x3, k1, k2, k3, m]
circ[p_, p0_, r_] := (p - p0) . (p - p0) - r^2
(*** ELEMENTS INVOLVED ***)
r1 = 1;
p = {x, y};
circ1 = circ[p, {0, 0}, r1];
circ2 = circ[p, {r2 - r1, 0}, r2];
circ3 = circ[p, {2 r2 - r1 + r3, y3}, r3];
circ4 = circ[p, {2 r2 - r1 + r3, 0}, r3];
l2 = y - m (x - r1);
(*** TANGENCY POLYNOMIALS ***)
rc2l2 = First[Eliminate[{circ2 == 0, l2 == 0}, y]] - k1 (x - x1)^2;
rc4l2 = First[Eliminate[{circ4 == 0, l2 == 0}, y]] - k2 (x - x2)^2;
rc3l2 = First[Eliminate[{circ3 == 0, l2 == 0}, y]] - k4 (x - x4)^2;
rc3c1 = First[Eliminate[{circ1 == 0, circ3 == 0}, y]] - k3 (x - x3)^2;
(*** EQUIVALENT CONDITIONS ***)
res1 = CoefficientList[rc2l2, x];
res2 = CoefficientList[rc4l2, x];
res3 = CoefficientList[rc3c1, x];
res4 = CoefficientList[rc3l2, x];
equs = Join[Join[res1, res2], Join[res3, res4]];
vars = Variables[equs];
(*** ALGEBRAIC SOLUTIONS ***)
sols = Quiet@Solve[equs == 0, vars];
sols0 = Take[sols, {27, 28}];
elems = {circ2, circ3, circ4, l2} /. sols0;
(*** CONFIRMATION GRAPHICS ***)
GRS = {};
For[k = 1, k <= Length[elems], k++, For[j = 1, j <= 4, j++,
  AppendTo[GRS, 
   ContourPlot[elems[[k, j]] == 0, {x, -1, 1}, {y, -1, 1}]]
  ]
 ]
gr0 = Graphics[Circle[{0, 0}, 1]];
gr0a = Plot[r2 /. sols0[[2]], {x, -1, 1}, PlotStyle -> {Thin, Black, Dashed}];
gr0b = Plot[-r2 /. sols0[[2]], {x, -1, 1}, PlotStyle -> {Thin, Black, Dashed}];
Show[gr0, gr0a, gr0b, GRS, PlotRange -> All]