0

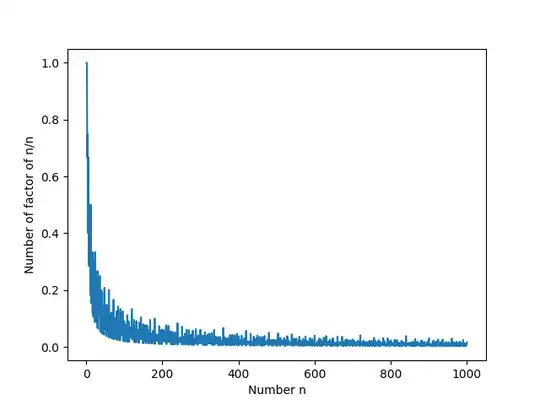
Given any $n$, can one determine the maximum number of factors that $n$ can have? I couldn't determine much mathematically, so I tried computing the result and I obtained this

Relationship between factors and numbers

The graph seems to be exponentially decaying, does there exist any closed form or inequality that relates number of factors of $n$ and $n$?

(PS : I need the upper bound for increasing the computational efficiency of a different related problem)

Aadi
  • 824
  • 2
    Check this: https://math.stackexchange.com/q/3043181/42969 – Martin R Jun 16 '24 at 07:24
  • Ohk, thanks...... – Aadi Jun 16 '24 at 07:28
  • Please clarify "number of factors" , do you count the divisors or only the prime factors , exclude or include the nontrivial factors etc. – Peter Jun 16 '24 at 07:28
  • 1
    Divisors........ – Aadi Jun 16 '24 at 07:28
  • 1
    Lots of information at the Wikipedia article: https://en.wikipedia.org/wiki/Divisor_function#Growth_rate – Qiaochu Yuan Jun 16 '24 at 07:29
  • Dissertation of G. Robin: With equality at $n = 6983776800 $ and $d(n) = 2304,$ $$ d(n) \leq n^{ \left( \frac{\log 2}{\log \log n} \right) \left( 1.5379398606751... \right)} = n^{ \left( \frac{1.0660186782977...}{\log \log n} \right) }. $$

    With equality at a number $n$ near $6.929 \cdot 10^{40},$ $$ d(n) \leq n^{ \left( \frac{\log 2}{\log \log n} \right) \left( 1 + \frac{1.934850967971...}{\log \log n} \right)}. $$ Compare this one with Theorem 317 in Hardy and Wright, attributed to Wigert (1907), $$ \limsup \frac{\log d(n) \log \log n}{\log n} = \log 2. $$

     – Will Jagy Jun 16 '24 at 14:08

0 Answers0