1

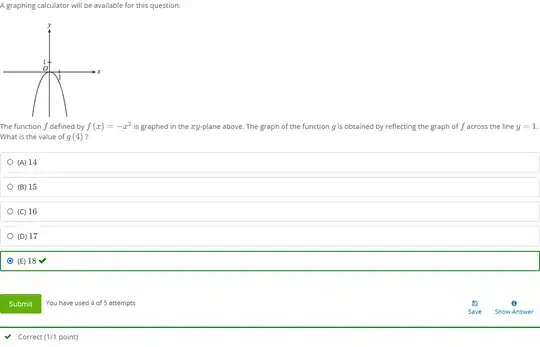
I have the answer, but I am interested in the process by which it is obtained because in the textbooks I've used, they tend not to have questions such as this one. I find this question rather tricky.

If I were to find another questions like this say instead of $f(x)$ being reflected across the $y$-axis at 1, it says instead, it's reflected across the y-axis at 3. Would the answer be 22, in that case.

The limit for the question field for this post restricted me to a truncated version of the question. I've attached a screenshot of the question below to more fully illustrate the context of the problem.

enter image description here

BSplitter
  • 1,719
David A.
  • 95
  • Can you not move the entire function down 1 unit to make the reflecting line $y=0$ and then do a fairly standard reflection in the $x$-axis? If so, this would work for $y=k$ as well. – Red Five Jun 14 '24 at 22:59
  • A more general case of reflecting in any line is given here: https://math.stackexchange.com/questions/1404960/reflecting-a-function-about-a-line?rq=1 – Red Five Jun 14 '24 at 23:00

5 Answers5

3

The way that I might approach this problem is to try and determine what the graph would look like after flipping it over the line $y=1$. Since the vertex of $f$ is at $(0,0)$, the vertex of $g$ must be at $(0,2)$. Then, I might ask myself what the function $g$ would be algebraically. Since $g$ is an upward facing parabola, and its vertex is at $(0,2)$, the graph of $g$ must be $g(x)=x^2+2$. Then find $g(4)$ from here, by plugging $4$ in.

BSplitter
  • 1,719
3

BSplitter's answer provides complete information about the function $g$, but if you only want to determine $g(4)$, then here's an alternative approach. First, note that reflection in a horizontal line won't change the $x$-coordinate of a point, so, since we want a point on the graph of $g$ with $x$-coordinate $4$, we should find the point on the graph of $f$ with $x$-coordinate $4$. The formula for $f$ says that is $(4,-16)$, which is $17$ units below the reflection line $y=1$. So its reflection, on the graph of $g$, will be $17$ ubits above that line, i.e., at height $18$.

Andreas Blass
  • 75,557
3

The image of $(x,y)$ under a reflection across the line $y = 1$ (which is a horizontal line) is given by

$ (x',y') = ( x , 1 - (y - 1) ) = (x , 2 - y) $

It follows that

$ (x, y) = (x', 2 - y') $

Since $ y = - x^2 $ , then

$ 2 - y' = - x'^2 $

i.e.

$ y' = 2 + x'^2 $

This is the relation governing the new reflected curve.

i.e

$g(x) = 2 + x^2 $

Now,

$g(4) = 2 + 4^2 = 2 + 16 = 18 $

0

Since no one else directly mentioned composition of functions as such, although that is the foundation of the answer of c'est pas normale, I will write such an answer.

$~f(x) = -(x^2).~$

Let $~g(x)~$ represent reflection across the line $~y = 1.~$

Then:

  • $~g(1) = 1 = (2 - 1).$

  • $g(x) = 1 - (x - 1) = 2 - x ~: ~x > 1.$

  • $g(x) = 1 + (1 - x) = 2 - x ~: x < 0.$

So, $~g(x) = (2 - x),~$ for all $~x.~$

Therefore, $~g[f(x)] = g[ ~-(x^2) ~] = 2 - [ ~-(x^2) ~] = 2 + x^2.$

Therefore, $~g[f(4)] = 2 + 4^2.$

user2661923
  • 42,303
  • 3
  • 21
  • 46
0

$$\Large \color{red}{g(4)=2\cdot1-f(4)=2+4^2=18}$$

The reflection of $y=f(x)$ over the line $y=k$ is equivalent to the reflection over the $x-$axis ($y\rightarrow-y$), followed by the translation upwards with $2k$ units ($-y\rightarrow-y+2k$). $$\large y=f(x)=-x^2\xrightarrow[\text{over}~\color{red}{y=1}]{\text{Reflection}}\color{red}{(2\cdot1-y)}=-x^2\implies \color{red}{y=g(x)=x^2+2}$$ So, $$\Large \color{red}{\boxed{g(4)=4^2+2=18}}$$

Pustam Raut
  • 2,490