How to calculate $\int_{0}^{\infty} x^n(1+x)^n e^{-ncx^2}\text{d}x$

Question

As the title mentioned, I want to calculate \begin{equation} \int_{0}^{\infty} x^n(1+x)^n e^{-ncx^2}\text{d}x, \end{equation} where $n$ is a positive integer, $c$ is a positive real number in the maginitude of 1 (valued around 1).

This integral is difficult because of the term $(1+x)^n$, if we expand this term then the result can be written as \begin{equation} \frac12 \sum_{k=0}^{n} \binom nk (nc)^{-\frac{n+1+k}2}\Gamma(\frac{n+1+k}2), \end{equation} where the sum of Gamma function is also difficult to deal with. If the exact result is difficult, a strict upper bound is also welcomed, or an asymtotic bound w.r.t. $n\to \infty$.

Answer 1

To approach this problem from another direction, I'll dispense with exact results and instead seek an approximation via Laplace's method (though I will not purport to do so with much rigor).

To apply Laplace's method, we write the integral as $F_n(c)=\int_0^\infty e^{-n f(x)}dx$ where $$f(x,c):=-\ln x-\ln(1+x)+cx^2$$ The critical point is defined by $$\frac{\partial f}{\partial x}=2cx-\frac{1}{x}-\frac{1}{1+x}=0$$ If we rearrange to express this in terms of $c$, we obtain

$$c=\frac{1}{2x}^2+\frac{1}{2x(x+1)}$$

Both terms are decreasing functions of $x$ for all positive $x$, so in principle we can invert this to obtain $x$ in terms of $c$. However, for the present time I'll instead take the critical point $x_0$ itself to be the "parameter" and take $c$ to depend on $x_0$ as $c=(2x_0)^{-1}+(2x_0(x_0+1))^{-1}$$

With this understanding, we expand $f(x,c)$ about $x=x_0$ and obtain

$$f(x,c)\approx c x_0^2-\ln x_0-\ln(1+x_0) +\frac{(x-x_0)^2}{2}\left(2c+x_0^{-2}+(1+x_0)^{-2}\right)+$$

Extending the integration to $x=-\infty$ and evaluating the resulting Gaussian integral, we thus obtain the approximation

$$F_n(c) \approx x_0^n (1+x_0)^n e^{-n c x_0^2}\sqrt{\frac{2\pi/n}{2c+x_0^{-2}+(1+x_0)^{-2}}}$$

which we expect to be valid for large $n$. As a test of such, we specialize to the case $x_0=1$ in which case $c=3/4$. This yields

$$F_n(3/4)\approx (2e^{-3/4})^n\sqrt{\frac{8\pi}{11 n}}$$

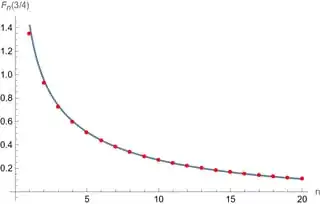
On the other hand, we can use Mathematica to explicitly evaluate the sum formula given by the OP for a range of integer $n$. This yields the following graph, where the blue curve is the approximation and the red dots are the actual values up to $n=20$:

This is remarkably good agreement, even down to $n=1$. It is, of course, only a test of one such value of $c$. However, experimenting with various values of $(x_0,c)$ suggests that it is robust for both large and small $c$. Hence this seems a reasonable approach to constraining the behavior of $F_n(c)$, at the cost of having to put up with $c$ being a function of $x_0$.

Answer 2

Since $n$ should is a positive integer, you should begin with

$$ (1+x)^n = \sum_{k=0}^n \binom{n}{k} x^k $$

Hence

$$ \int_0^\infty x^n(1+x)^n e^{-ncx^2} dx = \sum_{k=0}^n \binom{n}{k} \int_0^\infty x^{n+k} e^{-ncx^2} dx $$

One way of handling this is repeated integration by parts, starting with

$$ \int_0^\infty x^{n+k} e^{-ncx^2} dx = -\frac 1 {2cn} \int_0^\infty x^{n+k-1} \cdot (-2cxn) \cdot e^{-ncx^2} dx $$

You can continue from there.

Answer 3

The representation as a sum of two terminating hypergeometric series is $$ \int_0^\infty x^n(1+x)^n e^{-ncx^2}dx = \sum_{k=0}^n \binom{n}{k} x^{n+k} e^{-ncx^2}dx $$ $$ = \frac12 \sum_{k=0}^n \binom{n}{k} \frac{\Gamma((n+k+1)/2)}{(nc)^{(n+k+1)/2}} $$ $$ = \frac12 \sum_{k=0,2,4\ldots}^n \binom{n}{k} \frac{\Gamma((n+k+1)/2)}{(nc)^{(n+k+1)/2}} +\frac12 \sum_{k=1,3,5\ldots}^n \binom{n}{k} \frac{\Gamma((n+k+1)/2)}{(nc)^{(n+k+1)/2}} $$ $$ = \frac12 \sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k} \frac{\Gamma((n+2k+1)/2)}{(nc)^{(n+2k+1)/2}} +\frac12 \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k+1} \frac{\Gamma((n+2k+2)/2)}{(nc)^{(n+2k+2)/2}} $$ $$ = \frac{1}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k} \frac{\Gamma((n+2k+1)/2)}{(nc)^k} +\frac{1}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k+1} \frac{\Gamma((n+2k+2)/2)}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k+1} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{\Gamma(n+1)}{\Gamma(1+2k)\Gamma(n-2k+1)} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \frac{\Gamma(n+1)}{\Gamma(2+2k)\Gamma(n-2k)} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{1}{(1)_{2k}(n+1)_{-2k}} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \frac{n}{(2)_{2k}(n)_{-2k}} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{1}{(1/2)_k(1)_k2^{2k}(n+1)_{-2k}} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \frac{n}{(1)_k(3/2)_k2^{2k}(n)_{-2k}} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{(-n)_{2k}}{(1/2)_k(1)_k2^{2k}} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \frac{n(1-n)_{2k}}{(1)_k(3/2)_k2^{2k}} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{(-n/2)_k(-n/2+1/2)_k2^{2k}}{(1/2)_k(1)_k2^{2k}} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \frac{n(1/2-n/2)_k(1-n/2)_k2^{2k}}{(1)_k(3/2)_k2^{2k}} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}} \sum_{k=0}^{\lfloor n/2 \rfloor} \frac{(-n/2)_k(-n/2+1/2)_k}{(1/2)_k(1)_k} \frac{((n+1)/2)_k}{(nc)^k} +\frac{\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} \sum_{k=0}^{\lfloor n/2\rfloor} \frac{n(1/2-n/2)_k(1-n/2)_k}{(1)_k(3/2)_k} \frac{((n+2)/2)_k}{(nc)^k} $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}}{}_3F_1(-n/2,-n/2+1/2,n/2+1/2;1/2;\frac{1}{nc}) +\frac{n\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} {}_3F_1(1/2-n/2,1-n/2,1+n/2;3/2;\frac{1}{nc}) $$ $$ = \frac{\Gamma((n+1)/2)}{2(nc)^{(n+1)/2}}{}_3F_1\left(\begin{array}{c}-\frac{n}{2},\frac{1-n}{2},\frac{1+n}{2}\\ \frac12 \end{array}\mid \frac{1}{nc}\right) +\frac{n\Gamma((n+2)/2)}{2(nc)^{(n+2)/2}} {}_3F_1\left(\begin{array}{c}\frac{1-n}{2},1-\frac{n}{2},1+\frac{n}{2}\\ \frac32\end{array}\mid\frac{1}{nc}\right) $$

Checking with maple to verify:

A := proc(n,c)
    local nc ;
    nc := n*c ;
    GAMMA((n+1)/2)/nc^((n+1)/2) * hypergeom([-n/2,-n/2+1/2,n/2+1/2],[1/2],1/nc) 
    +n*GAMMA(n/2+1)/nc^(n/2+1) * hypergeom([1/2-n/2,-n/2+1,n/2+1],[3/2],1/nc) 
    ;
    %/2 ;
    evalf(%) ;
end proc:
c :=1 ;
for n from 1 to 5 do
    A(n,c) ;
    print(n,%) ;
end do:

which agrees with the original terms:

1, 0.9431134627263790068245418708352862956993873640305967820534519474632278211477580453437376641846361662
2, 0.5241624675377656799517243280262080745476391747542120033813978911624383684727327160097839198226000135
3, 0.3301146825192308002432617178642575819185392921407806468356754186529366158769580473065306455515915153
4, 0.2193960916974432250831443072850308014468449583054484685909083570727789780535326982701614268739685012
5, 0.1502852356531458786478215699552018675321911055849259103478390039883172150130134000461991269890007667

With equation (2.2.3.2) of the book by Lucy Joan Slater "Generalized hypergeometric Functions" the two 3F1 terms can be rewritten as 2F2 terms.