6

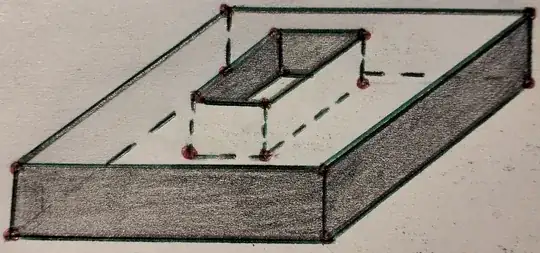
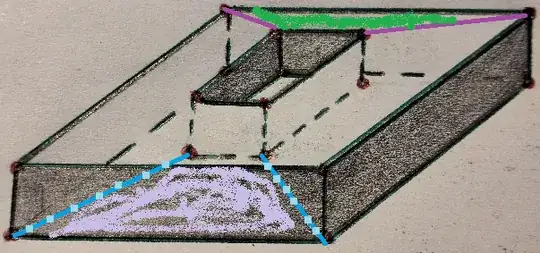
Why is it that when I try to compute the Euler characteristic for the Torus using a drawing like the following , then the number that I get is not the number that the Torus should have? Which is $0$?

I mean, if I understand correctly, given any polygon and counting $V-E+F$ then I get the Euler characteristic for that specific volume. But in my case, $V-E+F=16-24+10=2$.
Obviously, this torus is not the same as the sphere which has the same apparent Euler characteristic.

I know that there exists a way for creating a torus from a simple sheet of paper by identifying the corners of such, and in this case the Euler characteristic comes up being $0$ as it should.
But I just wanted to know what was the flaw in my argument.

Polygonal Torus

Prem
  • 14,696
Tutusaus
  • 667
  • "Given any polygon" - you have to define what a "polygon" means correctly. In your current drawing you are not using the right notion of a "polygon." (What you are counting as a top/bottom "face" is not a face by any standard topological definition.) – Moishe Kohan Jun 10 '24 at 15:08
  • Summary : "what was the flaw in my argument" : You can not have holes in the 2 faces, How to fix it ? You have to break the 2 "hole faces" into 2+2 faces without holes. It will change $F$. Naturally , that will change $E$ too , though $V$ will not change. – Prem Jun 10 '24 at 15:29
  • Maybe #faces is 8. – Bob Dobbs Jun 10 '24 at 15:44
  • Actually , #faces should be 12 , @BobDobbs , Details in my answer. – Prem Jun 10 '24 at 15:59
  • Did you have to add edges? @Prem – Bob Dobbs Jun 10 '24 at 16:01
  • 1
    Yes , that is necessary , @BobDobbs , though it is not necessary to add vertices. – Prem Jun 10 '24 at 16:03
  • Maybe migrate this question to the Blender site? :-) – Jos Jun 11 '24 at 11:27

2 Answers2

16

Euler Characteristic demands no holes in the faces (or rather , the formula changes when there are holes)

Here is a way to remove the holes on the top face and bottom face.

CHECK

We join 2 Pairs of existing vertices (Purple lines) to generate a new face in green on the top.
We like-wise join 2 Pairs of existing vertices (Blue lines) to generate a new face in grey at the bottom.
Now Euler Characteristic will work out.
$$V-E+F=16-28+12=0$$

[[
Copy-Pasting the gist of my earlier comment here , for quick reference :
Summary :
"what was the flaw in my argument" : You can not have holes in the $2$ faces.
How to fix it ? You have to break the $2$ "hole faces" into $2+2$ faces without holes. That will change $F$ , which will naturally change $E$ too , though $V$ will not change.
]]

Prem
  • 14,696
0

You should use Euler formula on a triangulation if you want to compute the euler characteristic. One easy triangulation of the torus can be obtained as following:
enter image description here

Obtained by "discretizing a donut".
Opening up the diagram one obtains (sorry for the drawing) enter image description here

from which you easily deduce that this particular triangulation has $9$ vertex, $27$ edges and $18$ faces.

Alessandro Fenu
  • 715
  • 4
    One does not need a triangulation, a CW complex structure would work just fine, this is what OP was trying to use (incorrectly). – Moishe Kohan Jun 10 '24 at 15:16