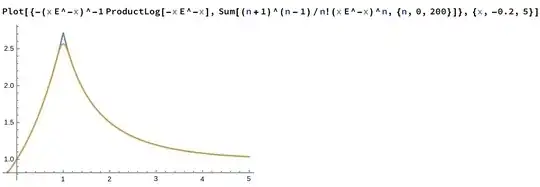
I need help to evaluate series :$$S(x)=\sum^{\infty}_{n=0} \frac{(n+1)^{n-1}}{n!}(xe^{-x})^n$$ My attempt was to find an integral equal to $\frac{(n+1)^{n-1}}{n!}$ But I couldn't find it
This is what I found but I don't know if it might help solve this problem
$$\int^{\infty}_0 x^{n}e^{-nx} dx =\frac{n!}{n^{n+1}} $$
$\DeclareMathOperator WW$The Lambert W series expansion is known to be:
$$\sum_{n=1}^\infty\frac{(-n)^{n-1}x^n}{n!}=\W(x),|x|<\frac1e$$
then shifting the index $n\to n+1$ and using $(n+1)n!=(n+1)!$ gives:
$$\sum_\limits{n=0}^\infty\frac{(n+1)^{n-1}}{n!}x^{n+1}=-\W(-x)$$
meaning
$$\begin{align}\sum^{\infty}_{n=0} \frac{(n+1)^{n-1}}{n!}(xe^{-x})^n=-\frac{e^x}x\W(-xe^{-x}),x>-\W(e^{-1})\\=e^x,-\W(e^{-1})<x<1\end{align}$$
as shown here:
