A Special Chart
Locally, a chart of $X$ could be $$\begin{align*}
\phi \colon X &\to \mathbb{R}^{2} \\
(x,y,z) &\mapsto (u,v),
\end{align*}$$
such that
$$ x=ue^{-\frac{1}{u^2+v^2}},y=ve^{-\frac{1}{u^2+v^2}}.$$
We define $e^{-\frac{1}{0^2+0^2}}$ to be zero.
To show that this is indeed a homeomorphism, it suffices to prove the following map
$$\begin{align*}
F \colon \mathbb{R}^{2} &\to \mathbb{R}^{2} \\
(u,v) &\mapsto \exp \left(-\frac{1}{u^{2}+v^{2}} \right)\cdot (u,v)
\end{align*}$$
is a homeomorphism. We only need to prove $F^{-1}$ is continuous at the origin.
The map $F^{-1}$ is continuous at $0$ iff $\forall \epsilon>0, \exists \delta >0$, such that $F^{-1}(B_\delta (0))\subset B_\epsilon(0)$. It is equivalent to proving $\forall \epsilon>0, \exists \delta >0$, such that $e^{-\frac{2}{r^2}}r^2<\delta^2\implies r^2<\epsilon^2$. Choosing $\delta^2=\frac{1}{2} \epsilon^2 e^{-\frac{2}{\epsilon^2}}$ will do the job.
A chart of $\mathbb{R}^{3}$ is
$$
\begin{align*}
\operatorname{id} \colon \mathbb{R}^{3} &\to \mathbb{R}^{3} \\
(x,y,z) &\mapsto (x,y,z).
\end{align*}
$$
Now, the representation of the inclusion map is $$\begin{align*}
\operatorname{id}\circ i \circ \phi^{-1} \colon \phi(X) &\to \mathbb{R}^{3} \\
(u,v) &\mapsto (u\exp\left(-\frac{1}{u^2+v^2}\right),v\exp\left(-\frac{1}{u^2+v^2}\right),\exp\left(-\frac{1}{2(u^2+v^2)}\right)(u^2+v^2)^{1/4}).
\end{align*}$$
Smoothness
Now, we will prove that $z=\exp\left(-\frac{1}{2(u^2+v^2)}\right)(u^2+v^2)^{1/4}$ is smooth at $(0,0)$. In fact, the higher-order derivatives of $z$ are all $0$. The idea is the same as taking the n-th derivative of $f(x)=e^{-\frac{1}{x^2}}$ at $0$.
Let's first calculate the first-order derivative of $z$ at the origin.
$$\begin{aligned}\frac{\partial z}{\partial u}\Bigg|_{(0,0)}&=\lim_{u\to 0}\frac{\exp\left(-\frac{1}{2(u^2+0^2)}\right)(u^2+0^2)^{1/4}-0\cdot (0^2+0^2)^{1/4}}{u}\\
&=\pm \lim_{|u|\to 0^+}\frac{\exp\left(-\frac{1}{2u^2}\right)}{\sqrt{|u|}}\\
\left(t=\frac{1}{\sqrt{|u|}}\right):\;&= \pm \lim_{t\to +\infty} \frac{t}{\exp \left({\frac{t^4}{2}}\right)}\\ \left(
\text{L'Hôpital's rule} \right):\;&=\pm \lim_{t \to \infty} \frac{1}{2 e^{\frac{t^4}{2}} t^3}\\ &= 0 \end{aligned}$$
Similarly, we have $$\frac{\partial z}{\partial v}\Bigg|_{(0,0)}=0.$$
We can now use mathematical induction to prove $$z^{(m,n)}|_{(0,0)}\equiv \frac{\partial^{m+n} z}{\partial^m u \;\partial^n v}\Bigg|_{(0,0)}=0.$$
When $(u,v)\neq (0,0)$, the $(m,n)$-th derivative has the form
$$z^{(m,n)}\equiv \frac{\partial^{m+n} z}{\partial^m u \;\partial^n v}=\exp\left(-\frac{1}{2(u^2+v^2)}\right)\frac{P(u,v)}{(u^2+v^2)^{\frac{s}{4}}},$$
where $s$ is an integer and $P(u,v)$ is some polynomial of $u,v$.
For example,
$$z^{(2,1)}\equiv \frac{\partial^{2+1} z}{\partial^2 u \;\partial^1 v}=\frac{\exp\left(-\frac{1}{2 \left(u^2+v^2\right)}\right)}{(u^2+v^2)^{23/4}} \cdot \frac{v}{8} \left(15 u^8+3 u^6 \left(13 v^2+34\right)+u^4 \left(27 v^4+180 v^2-76\right)+u^2 \left(-3 v^6+54 v^4-68 v^2+8\right)-6 v^8-24 v^6+8 v^4\right)$$
Given $z^{(m,n)}|_{(0,0)}=0$, we have
$$\begin{aligned}z^{(m+1,n)}|_{(0,0)}&=\lim_{u\to 0}\frac{z^{(m,n)}(u,0)-0}{u}\\
&=\lim_{u\to 0} \exp\left(-\frac{1}{2(u^2+0^2)}\right)\frac{P(u,0)}{u\cdot (u^2+0^2)^{\frac{s}{4}}}\\
\left(t=\frac{1}{\sqrt{|u|}}\right):\;&= \pm P(0,0)\cdot \lim_{t \to \infty}\frac{t^{s+2}}{\exp \left({\frac{t^4}{2}}\right)}\\\left(\text{L'Hôpital's rule} \right):\;&=\pm P(0,0)\cdot \lim_{t \to \infty}\frac{(s+2)!}{\exp \left({\frac{t^4}{2}}\right)p(t)}\\&=0,\end{aligned}$$
where $p(t)$ is just a polynomial. Similarly, you can prove $z^{(m,n+1)}|_{(0,0)}=0$.
Therefore, by the principle of induction, $z^{(m,n)}|_{(0,0)}=0$ for all integers $m,n$, and the $z(u,v)$ is smooth at the origin.
Intuitions
Next, we will interpret our results, and gain some intuition.
First, let's see what $z^4=x^2+y^2$ looks like:
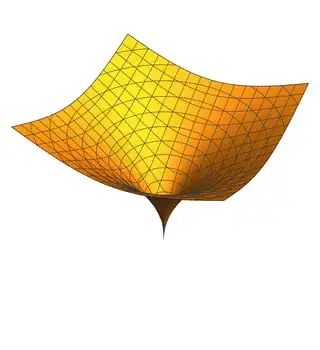
Clearly, the origin is a critical point.
Let's see what $z^4=\exp\left(-\frac{2}{u^2+v^2}\right)(u^2+v^2)$ looks like:
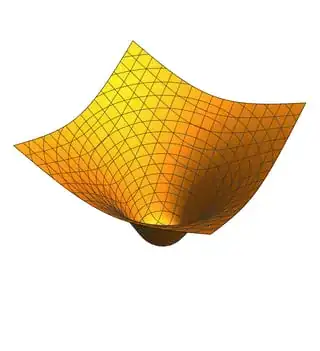
The origin is now smooth.
You may wonder why these two charts are so different; this is because our homeomorphism $F$ is not a diffeomorphism.
To make this point more precise, let's calculate the Jacobian of $F$ at the origin:
$$ JF|_{(0,0)}= \begin{pmatrix}
0 & 0 \\
0 & 0 \\
\end{pmatrix} ,$$
so $JF^{-1}|_{(0,0)}$ doesn't exist. That is to say, $F^{-1}$ is only continuous, but not differentiable.
However, any point other than $(0,0)$ is differentiable:
$$ JF|_{(u,v)\neq (0,0)}= \frac{e^{-\frac{1}{u^2+v^2}}}{(u^2 + v^2)^2}\begin{pmatrix}
u^4+2 u^2
\left(v^2+1\right)+v^4 & 2
u v \\
2 u v & u^4+2 v^2( u^2+1)+v^4
\end{pmatrix}, $$
and
$$\det JF|_{(u,v)\neq (0,0)}= \frac{e^{-\frac{2}{u^2+v^2}}
\left(u^2+v^2+2\right)}{u^2
+v^2}>0.$$
By the Inverse function theorem, $F^{-1}|_{(u,v)\neq (0,0)}$ is smooth.

