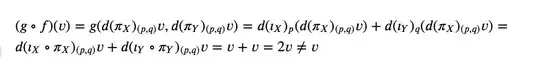I am trying to check the following claim:
All the books I found that mention this do not give a prove. Here I found the proof that it is a left inverse:
Tangent Space of Product Manifold. (*)
I tried to show that it also a right inverse, which is basically what is done here:
https://unapologetic.wordpress.com/2011/04/27/the-tangent-space-of-a-product/
How does the marked equation above follow from the relations stated above it? Why is the order of the projection and the insertion map reversed? That's not by the chain rule, is it?
I ran into the same problem as in (*) namely:
Apparently $d(i_X\circ\pi_X)\neq Id$ or in the notation of the book I use $d(i_p\circ\Pr_1)\neq Id$ , which puzzles me, because if I look at $i_q\circ\Pr_1(p,q)=i_q(p)=(p,q)$.
Many thanks in advance!