In the figure, $OP = 1$ and $PF = 3$. Calculate $r$.
$DC$ and $DE$ are tangents. (Answer:$r=2$)
Could this issue be resolved only with this data?
I try:
$Point Theorem: FA.FB = FC.FE \implies (3-(r-1).(4+r) = FC.(FC+FE)$
$DC=DE$
$\triangle AEB: AE^2+EB^2 =(2r)^2 = 4r^2$
Let $DO=x$
Using triangle similarity in $\triangle DOP$ and $\triangle FOK$,
$$KO=\frac{4}{x}$$
Thus, $$DK=DO-KO=\frac{x^2-4}{x}$$
Using the Geometric mean theorem in the right angled triangle $\triangle DOC$,
$$CK=\sqrt{DK\cdot KO}=\sqrt{\frac{4(x^2-4)}{x^2}}$$
Now, using the Pythagorean theorem in the right-angled $\triangle COK$,
$$\boxed{r=CO=2}$$
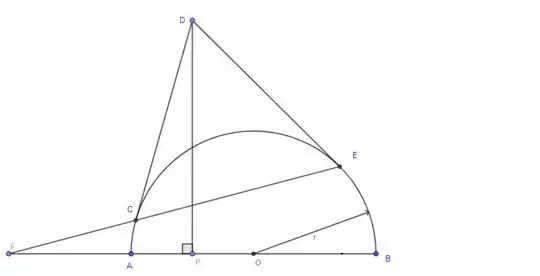
Yes these values allow to have a unique answer.
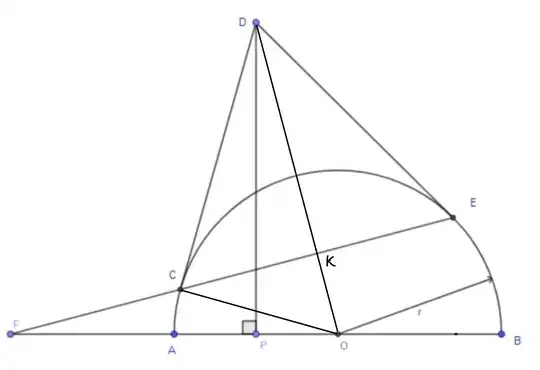
Let $G$ be the intersection of line $PD$ with the circle.
Draw the upper tangent issued from $F$ to the circle. Its point of tangency is exactly $G$ (by the duality property of polarity (See Edit below) :
$$\text{Point} \ F \ \leftrightarrow \ \text{Line} \ (F) = \text{ Line } \ PD$$
$$\text{Point} \ D \ \leftrightarrow \ \text{Line} \ (D) = \text{ Line } \ CE$$
Let us recall the important property : if the polar line of any point $M$ (here $D$) with respect to a circle passes through $N$ (here $F$) then, in a symmetrical way, the polar line of $N$ (here $F$) passes through $M$ (here $D$). Then this polar line is $PD$ and its intersection $G$ with the circle is the point of tangency.
$FG$ being a tangent in $G$, it is orthogonal to radius $OG$, which means that triangle $OGF$ is a right triangle.
If we apply in this triangle the Geometric Mean Theorem : the altitude issued from the right angle vertex is the Geometric Mean of the lengths of the sides determined by its foot on the hypotenuse, we get :
$$PG=\sqrt{PO.PF}=\sqrt{3}$$
Now consider right triangle $OPG$ and apply Pythagoras to it.
Edit : In a very short way : what is polarity ?
Let us explain it wrt the unit circle. It is an "hybrid" transformation exchanging :
$$\text{Point} \ P \ \leftrightarrow \ \text{Line} \ (P)\tag{1}$$
where, in the case where $(P)$ is exterior to the circle is the line obtained by joining the two points of tangency of the tangents issued from $P$ (for example, on the figure above, the polar line of $D$ is line $CE$)
There is a parallel analytical definition, which is more general
$$\text{Point} \ P (a,b) \ \leftrightarrow \ \text{Line} \ (P) ax+by=1\tag{1'}$$
This transformation has many properties, some of them being the consequence of the following duality property :
$$\begin{cases}\text{Point} \ A \leftrightarrow \text{Line}(A)\\\text{Point} B \ \leftrightarrow \text{Line} (B)\end{cases} \ \ \ \implies \ \ \ \text{Line} \ AB \leftrightarrow \ \text{Point} \ (A) \cap (B)$$
Partial answer:
After you have somehow proven that when the point $E$ varies, $D$ stays on a straight line perpendicular to $FB$ (which is what Jean-Marie has done in her answer), we may then define the point $G$ to be the intersection of $DP$ and the circle. Then consider what happens as $E\to G:\ C\to G$ also, and $D\to G.$ We see that $FG$ is tangent to the circle, and since $GO=r,$ it follows that $\angle FGO = 90^{\circ}.$
Let $h:=GP.$ It is elementary to prove that $\triangle FGP$ and $\triangle GOP$ are similar: $ \angle GPF = \angle GPO = 90^{\circ};\ \angle FGO = 90^{\circ}\implies\angle FGP = 90^{\circ} - \angle PGO = 180^{\circ} - (90^{\circ} + \angle PGO) = \angle GOP,\ $ and finally $\angle PFG = 180^{\circ} - (90^{\circ} + \angle FGP) = 180^{\circ} - (90^{\circ} + \angle GOP) = \angle PGO.$ Therefore the two triangles are similar. We thus have: $3:h = h:1\implies \frac{3}{h} = \frac{h}{1} \implies h^2 = 3.$ Furthermore, $1^2 + h^2 = r^2.$ Therefore, $r^2 = 1^2 + 3 = 4,\implies r = 2.$
Connect the points $F$ and $O$ to the point $D$. Also, join $C$ and $O$. Let $OD$ bisect $CE$ at $M$. Note that $OM\perp CE$, $DM\perp CE$, and $OC\perp DC$. We have $OF=OP+PF=1+3=4,\ FA=OF-OA=4-r$, and $FB=OF+OB=4+r$.
By the power of a point theorem, $$FA\cdot FB=FC+FE=FC(FC+2CM)$$$$\implies FC^2+2FC\cdot CM=(4-r)(4+r)=16-r^2\tag{1}$$
From the right-angled triangles $\triangle DPF$ and $\triangle DPO$, we can write $$DF^2=PF^2+DP^2=3^2+DO^2-OP^2$$ $$\implies DF^2=3^2-1^2+DO^2=8+DO^2\tag{2}$$
Similarly, from the right-angled triangles $\triangle DMF$, $\triangle DMC$ and $\triangle DCO$, we can write $$DF^2=FM^2+DM^2=(FC+CM)^2+DC^2-CM^2$$ $$\implies DF^2=FC^2+2FC\cdot CM+DO^2-r^2\tag{3}$$ From the equations $(1),\ (2)$ and $(3)$, we have $$8+DO^2=16-r^2+DO^2-r^2=16-2r^2+DO^2\implies r^2=4\implies \boxed{r=2}$$
Hence, the required radius of the circle is $2$ units.
Hope this helps!
