1

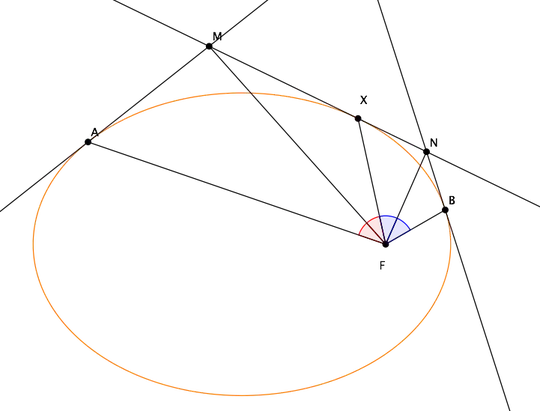
Let $A,B$ be two fixed points on the ellipse $\mathcal{E}$ and $X$ a movable point moving along the ellipse $\mathcal{E}$. Let $M,N$ be the intersections of the tangent to $\mathcal{E}$ passing through $X$ with the tangents to $\mathcal{E}$ passing through $A;B$. Show that, given one of the ellipse foci $F$, the lines $FM$, $FN$ form a constant angle.

I know that the tangent to an ellipse $\mathcal{E}$ passing through $P \in \mathcal{E}$ is the bisector of one of the angles formed by the lines $PF,PF'$, where $F,F'$ are the foci of the ellipse; but I can't relate this property to this problem. Any suggestions?

J P
  • 1,152

1 Answers1

1

This follows from this property of conics (see here for a proof):

If two tangents are drawn to a conic from an external point, then they subtend equal angles at the focus.

That means, in your case, that:

$$ \angle AFM=\angle XFM \quad\text{and}\quad \angle BFN=\angle XFN. $$

On the other hand we have (if $X$ lies inside $\angle AFB$): $$ \angle AFB=\angle AFM+\angle XFM+\angle XFN+\angle BFN= 2(\angle MFX+\angle XFN)=2\angle MFN $$ i.e. $\angle MFN$ is constant because it is one half of $\angle AFB$.

For the other positions of $X$ the same can still be proved, but with slight changes in the above equality. I leave to the reader discussing all possible cases.

enter image description here

Intelligenti pauca
  • 55,765