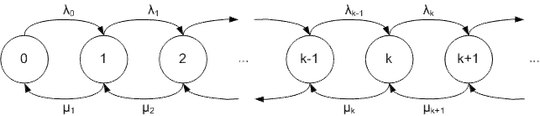
I am learning about Birth and Death (Stochastic) Processes (https://en.wikipedia.org/wiki/Birth%E2%80%93death_process):
When a birth occurs, the process goes from state $n$ to $n + 1$. When a death occurs, the process goes from state $n$ to state $n - 1$. The process is specified by positive birth rates$\{\lambda_i\}_{i=0\dots\infty}$ and > positive death rates $\{\mu_i\}_{i=1\dots\infty}$. The number of individuals in the process at time $t$ is denoted by $X(t)$. The process has the Markov property and $P_{i,j}(t)=\mathsf{P}\{X(t+s)=j|X(s)=i\}$ describes how $X(t)$ changes through time. For small $\triangle t>0$, the function, $P_{i,j}(\triangle t)$ is assumed to satisfy the following properties:
$$P_{i,i+1}(\triangle t) = \lambda_i \triangle t + o(\triangle t), \quad i \geq 0$$ $$P_{i,i-1}(\triangle t) = \mu_i \triangle t + o(\triangle t), \quad i \geq 1$$
$$P_{i,i}(\triangle t) = 1 - (\lambda_i + \mu_i) \triangle t + o(\triangle t), \quad i \geq 1$$
The way I see it, in each infinitesimal time unit, the Birth and Death process describes the probability of net population change. Assuming a fixed birth rate and death rate, the dynamics of the process can be described as follows. The probabilities $p_n(t)$ of being in state $n$ at time $t$ satisfy the following differential equations (Kolmogorov):
$$ \begin{align*} \frac{dp_0(t)}{dt} &= -\lambda_0 p_0(t) + \mu_1 p_1(t), \\ \frac{dp_n(t)}{dt} &= \lambda_{n-1} p_{n-1}(t) - (\lambda_n + \mu_n) p_n(t) + \mu_{n+1} p_{n+1}(t) \quad \text{for } n \geq 1. \end{align*} $$
Here:
- $\lambda_n$ for $n \geq 0$ and death rates $\mu_n$ for $n \geq 1$,
- $\lambda_n$ is the rate of "births" or transitions from state $n$ to state $n+1$,
- $\mu_n$ is the rate of "deaths" or transitions from state $n$ to state $n-1$,
- $p_n(t)$ is the probability of being in state $n$ at time $t$.
Based on this, I am trying to understand the following questions:
- How is the Birth and Death Process related to the Poisson Process?
- When will the next Birth and Death happen? Is this somehow related to the Exponentially Distributed Holding/Sojourn time of a Continuous Markov Chain, or the Exponentially Distributed Interarrival Times of a Poisson Process?
I know that a Poisson Process can be defined as:
$$\mathsf{P}(X(t) = k) = \frac{(\lambda t)^k e^{-\lambda t}}{k!}, \quad k = 0, 1, 2, \ldots$$ $$ \mathsf{P}[N(t + \Delta t) - N(t) = 1] = \lambda \Delta t + o(\Delta t)$$
I am guessing that in a Birth Death process, the number of births and deaths each follow a Poisson Process? Using the standard properties of a Continuous Time Markov Chain, I am guessing that in a Birth Death process:
- The time until the next event (either a birth or a death) when in state $n$ is exponentially distributed with parameter $\lambda_n + \mu_n$ (this is like a holding/sojourn time)
- The probability that the next event is a birth (transition to state $n+1$) is given by $\frac{\lambda_n}{\lambda_n + \mu_n}$.
- The probability that it is a death (transition to state $n-1$) is given by $\frac{\mu_n}{\lambda_n + \mu_n}$
Is my understanding correct? Is it possible to derive these formulas?