I'm pretty sure this series is divergent because $|\frac{\sin{kx}}{k}| \leq \frac{1}{k}$, which is a divergent harmonic series. I'm not sure on how to formally prove this, i thought about using the Cauchy criterion for uniform convergence, but i didn't get anywhere. Series are a new topic for me, any help?
Asked
Active
Viewed 94 times
-1
-
1How are you 'pretty sure'? Your 'argument' $|\frac{\sin{kx}}{k}| \leq \frac1k$ indicates nothing. – Anne Bauval May 21 '24 at 18:20
-
1Note that $\frac1{k^2} < \frac1k$ but this doesn't imply $\sum_{k=1}^\infty \frac1{k^2}$ diverges. – CyclotomicField May 21 '24 at 18:21
-
Try using summation by parts. – Mark Viola May 21 '24 at 18:34
-
1See https://math.stackexchange.com/questions/399238 Btw, before asking about uniform convergence, you should tell us what you know about pointwise convergence. – Anne Bauval May 21 '24 at 18:39
1 Answers
1
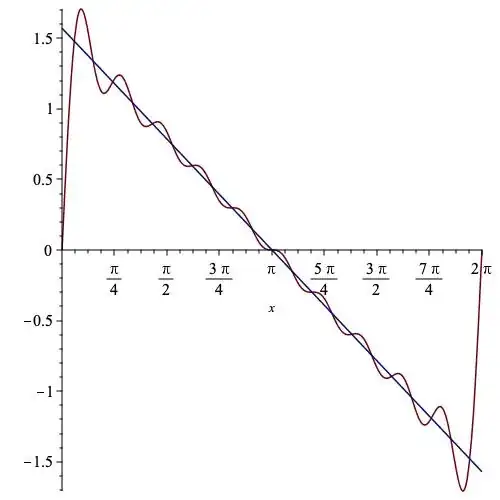
Hint. Graph a partial sum and the limit. Ask yourself whether they are uniformly close to each other.
GEdgar
- 117,296
-
I tried graphing the partial sum and iI got a similar graph, however I still don't understand how do i formally prove the divergence. If the series were convergent and $\sum_{k=1}^{\infty}\frac{1}{k}$ were convergent i would use the Weierstrass criterion to prove the convergence of the original series. – user1263607 May 21 '24 at 19:13
-
In Fourier series, the presence of a discontinuity induces the so-called "Gibbs phenomenon" ("overshoot") preventing uniform convergence. – Jean Marie May 21 '24 at 21:05
-
The picture shows that, near the endpoints, the two graphs are far,far apart (approximately $\pi/2$ and $0$). If we show that is true for every partial sum, then we know that convergence it not uniform. – GEdgar May 22 '24 at 01:13
-
-
I think, in this case, the OP can answer his question without knowing the Gibbs phenomenon. But of course the OP may want to look it up for future reference. – GEdgar May 22 '24 at 10:32